
福尔摩斯探案集《血字的研究》中提到的“演绎法”,至今让我印象深刻,
斯坦弗给我们介绍说:“这位是华生医生,这位是福尔摩斯先生。”
“您好。”福尔摩斯热诚地说,一边使劲握住我的手。我简直不能相信他会有这样大的力气。“我看得出来,您到过阿富汗。”
我吃惊地问道:“您怎么知道的?”
是一种由一般到特殊的推理方法。
如果一般性的结论成立,那么对于特殊的个体而言,结论也成立。
下面我们来看一下福尔摩斯是怎么推理的。
在你这件事上,我(福尔摩斯)的推理过程是这样的:
这一位先生,具有医务工作者的风度,但却是一副军人气概。那么,显见他是个军医。他是刚从热带回来,因为他脸色黝黑,但是,从他手腕的皮肤黑白分明看来,这并不是他原来的肤色。
他面容憔悴,这就清楚地说明他是久病初愈而又历尽了艰苦。他左臂受过伤,现在动作看来还有些僵硬不便。
试问,一个英国的军医在热带地方历尽艰苦,并且臂部负过伤,这能在什么地方呢?自然只有在阿富汗了。
福尔摩斯掌握了很多类似的“一般性结论”,
因此可以用求“交集”的办法,得到唯一确定的结论。
它是一种由特殊到一般的推理方法。
通过对个体特征进行总结,得出所有个体都满足的一般性规律。
中学时代,我们学到的数学归纳法,就是归纳推理的一个应用。
以上推理方法都是严谨的,但是现实生活中却经常遇到不严谨的场景,
因此,我们需对论证本身有所警觉,
避开一些常见的思维陷阱。
论证的四种可能性
可证明
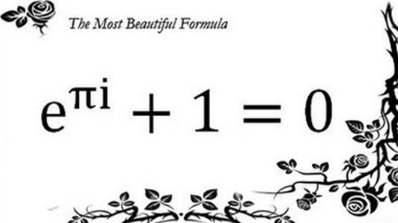
在数学上,人们追求的是可被证明的命题,
要么为真,要么为假,
未被证明的命题,是不可靠的,只是一种猜想。
已被证明为假的数学命题,给后辈节省了很多不必要的精力,
可证伪

然而,对于自然科学,上面的研究方法就不再适用了,
因为自然界是无穷无限的,总会探索到以前没有探索到的事情。
所以,科学方法提供了另一种研究手段。
科学方法是一种有系统地寻求知识的程序,涉及了以下三个步骤:
(1)问题的认知与表述
(2)实验数据的收集
(3)假说的构成与测试
科学方法通过不断修正理论的方式,逼近事实的真相。
对科学理论(或假说)的唯一要求就是,它必须是可证伪的。
一个理论被称为科学的,那么就必须先指明,什么样的观测反例,能证明它是错的。
如果一个理论无法被证明是错的,它就没有被推翻(修正)的可能。
例如,伽利略的比萨斜塔实验,证否了亚里士多德“重物先落地”的理论描述,
水星的近日点进动现象,证否了牛顿的万有引力定律(的适用性)。
可计算
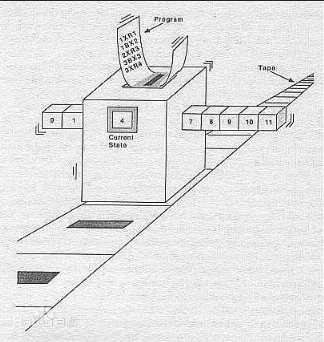
来到计算机科学,事情就又有些不同了,
计算机科学家们除了关心“能不能”之外,还会关心“成本”,
包括处理问题所需的“时间成本”,或者是“空间成本”。
有些事情是计算机没办法处理的,还有一些是处理起来代价过高的,
因此,在计算机科学中,人们关心的是可计算性,以及计算复杂度。
例如,停机问题就是不可计算(不可判定)的。
即,找不到一个通用算法,可以判定(回答“是”或者“不是”)任给的程序在有限的时间之内停机。
除了可计算性之外,NP完全问题描述了一类问题的复杂性,
它们的解,甚至(还没被证明)无法在多项式时间验证其正确性(NP问题)。
例如,旅行推销员问题,给定一系列城市和城市之间的距离,
求解访问每一座城市一次,并回到起始城市的最短路径。
算法的时间复杂度是指数级的。
小结
简而言之,数学是可证明的,科学是可证伪的,计算机科学是可计算的。
不幸的是,现实生活中很多在探讨中的问题,却并不具有这些良好的品质。
例如,常见的段子“PHP是最好的编程语言”,
这个问题是不可证伪的。
什么是“好”,什么是“不好”,根本没有统一的标准。
仅通过分析代码,想得出程序所有可能的运行时错误,
这个问题是不可判定的(不可计算的),
它就好像自然科学中的“永动机”一样,纠结这种问题是白费力气。
这些例子看起来是很可笑,似乎不可能有人会中招,
其实并非如此,
与它们等价的一些“可笑问题”,困扰了太多的人。
良好的开端

在讨论一个问题之前,应该先下定义,保证大家在讨论一个东西。
这件事看起来简单,其实是最难的。
比如,在讨论代码好坏的时候,很少有人会先定义“什么是好代码”。
那么,在此基础上的任何讨论都失去了意义,
讨论的双方都是仅凭自己的喜恶来判断,浪费再多的时间也无法得出结论。
所以,先对问题的定义进行统一,是一个好习惯,
问题的定义方式,区分了问题的论证方式。
有些问题,明显是不可计算的,也有一些问题是不可证伪的。
例如,寻找(或过分相信)强大的类型系统,
使得具备这种类型系统的编程语言,写出来的的程序没有运行时错误。
或者,我们要做一款产品,满足所有用户的需求,
又不区分哪些人是我们的用户。
且不说实现的难度,有些问题只看定义就知道是个陷阱。
可到达的终点

除了定义之外,验收也是问题相关的重要一环,
不确定验收标准,问题就永远无法解决。
事实上,所有验收都是有默认标准的,只不过这个标准没有达成共识,
“这个需求很简单,具体实现我不管,明天上线”。
这就是一个很好的没有确定“上线标准”的例子。
只说了明天上线,但是没有确定以什么标准上线,这是有风险的。
另外,在与上下游进行合作的时候,
模糊的验收标准,也会带来很多麻烦。
一个系统如果对其依赖方没有管控,那么它的稳定性就会出问题。
很难想象一个“巨人”能站在“泥足”之上。
在合作之前,先确定达成什么条件才可以验收,会节省很多沟通成本。
结语
本文总结了论证的 4 种可能性,实际上是对问题进行了划分,
目的是避开那些徒劳无意义的问题,
把精力用在“可证明,可证伪,可计算”的问题上。
此外,在讨论问题之前,我们需关心两个方面:
(1)问题有没有清晰的定义
(2)验收标准是什么?
这样才能保证在跟别人合作时,不会出现理解不一致的情形。
少费一些口舌,多解决一些问题,早点回家。
落日绣帘卷,亭下水连空。知君为我新作,窗户湿青红。
长记平山堂上,欹枕江南烟雨,杳杳没孤鸿。
认得醉翁语,“山色有无中”。
一千顷,都镜净,倒碧峰。忽然浪起,掀舞一叶白头翁。
堪笑兰台公子,未解庄生天籁,刚道有雌雄。
一点浩然气,千里快哉风。