
回顾
为了解释简单类型化演算中项,
我们介绍了代数,
用代数中的载体来解释基本类型,
用载体上的函数集来解释类型为的所有函数。
但只是做这些对应关系,还是不够的,
我们还得证明,这样的解释是“足够多的”,
以保证每一个合法项的解释,都在这个代数中。
尤其是使用集合上的函数,来解释具有不动点的项时,
的条件应当适当放宽一些,它不一定恰好是函数集。
为此我们需要更抽象的,从语义角度定义函数是如何作用到它的参数上的。
1. 作用结构

从形式系统的角度来看,项的“应用”,是推导规则的一部分,
包括类型推导规则,,
还包括求值规则,。
项的“应用”,我们可以定义为代数上的一个作用结构(applicative structure)。
假设是一个类型为的项,
我们可以把它“应用于”类型为的项,
我们有,。
因此,代数上的一个作用结构,
指的是这样的一个映射,,
它将集合中的一个函数,以及集合中的一个元素,
映射成集合中的一个元素。
一个有效的作用结构,必须具有外延性条件(extensional),
即,,
如果对于任意的,都有,则必有。
它指出集合的两个函数,如果在下的作用效果相同,
那么它们必须是同一个函数。
2. 项的唯一解释

有了满足外延性条件的作用结构之后,
我们就可以归纳的定义出含义函数(meaning function)了,
(1)
(2)
(3)
(4)
(5),存在唯一的,使得,
,
其中,是满足指派的环境,
是一个映射,将项常量映射到所有并集的元素上,
使得,如果,则。
由于以上几个等式覆盖了所有的项,因此这样定义的含义函数是完全的。
并且由于它为每一个项都指定了确定的语义,因此它给出的解释方式也是唯一的。
它称为Henkin模型。
Henkin模型是可靠的,
设是的任意Henkin模型,
是可证的,是一个满足指派的环境,
则。
即,如果一个类型断言是可证的,则它在语义上也成立。
(关于完全性的讨论,略)
3. 例子

我们可以对具有单一类型的演算,定义它的Henkin模型,
令为自然数集,为所有从到的函数集合,
这称为自然数上的完全集合论函数体系,
(full set-theoretic function hierarchy over the natural number)。
我们通过,把函数,作用到参数上。
下面我们得出的语义。
由于该项是封闭项,选择什么样的环境都是无关紧要的。
根据上文“含义函数”的归纳定义,我们有,
唯一的,使得,
,
然后我们再来看下,,
唯一的,使得,
,
即,唯一的,使得,,。
那么这个唯一的,实际上就是了。
其中,是因为,
综合以上两个步骤,,
唯一的,使得,
,。
因此,的语义是一个恒等函数。
我们从语义上证明了以下等式,
。
4. 环境模型条件和组合模型条件
以上定义的作用结构称为满足环境模型条件(enviroment model condition),
依赖了环境这一附加概念。
它使得每一个合法的项,都有模型中一个唯一确定的数学对象与之对应。
由于项有“抽象”和“应用”双重复杂性,
所以,建立一个合理的解释也比较麻烦。
在《你好,类型》系列文章中,
我们介绍过组合子逻辑,我们知道可以将任意的项转换成对应的项,反之亦然。
因此,如果存在模型可以解释所有的项,那么使用它也就可以解释所有项了。
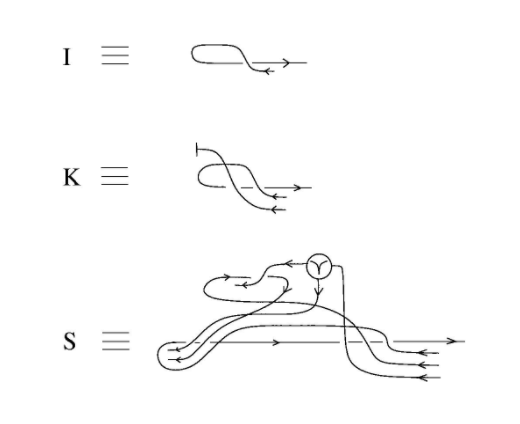
项比项更为简洁,它不包含“抽象”,只包含和这两个组合子。
类似于项的“应用”,
对于和的“组合”,我们同样可以定义代数上的一个作用结构。
给定代数,对任意类型,如果存在元素,
,
满足下列对合适类型的等式条件,
,,
我们就称,该作用结构满足组合模型条件(combinatory model condition)。
由于所有项都可以表示成和的“组合”,
因此,满足组合模型条件的作用结构,可以唯一解释所有项。
可以证明,一个满足外延性条件的作用结构,
如果它满足环境模型条件,当且仅当它也同样满足组合模型条件。
总结
本文介绍了Henkin模型作用结构所满足的条件,环境模型条件和组合模型条件,
它们是等价的,有了它们我们才能给出项的可靠解释,
即,任何合法的项都有唯一解释,且在语法上可证的项,在语义上也成立。
下文我们开始学习范畴论,为理解笛卡尔闭范畴打好基础。