
回顾
上一篇中,我们介绍了演算,
它是由一堆合法的符号和一些推导规则构成的公理系统,
在众多演算中,我们介绍了最常用的系统,
它指定了和两种对项的变换规则。
作为形式系统,上一篇中,我们展现了它的编码能力,
将邱奇编码,与公理集合论中自然数的归纳集定义,进行了对比。
本文我们将介绍另一套形式系统,
组合子逻辑(combinatory logic)。
1. 组合子逻辑
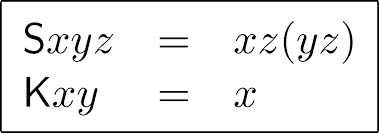
(组合子逻辑),与演算很相似,只是不需要对变量进行绑定,
和函数作用在值上不同的是,组合子作用在函数上,从而生成另一个函数。
例如,我们可以定义一个组合子,使得,其中,和都是函数。
为了避免过早的谈及语义,我们和演算一样,使用公理化的方法来定义它,
首先我们要说明什么是公理,即什么是合法的项,
(1)所有的变量,常量,以及组合子,,,都是合法的项,
(2)如果和是合法的项,那么也是。
例如,以下字符串都是合法的项,
,。
同样为了简化,某些情况下括号是可以省略的,如果我们默认各个项都是左结合的,
因此,可以简写为。
2. Weak reduction
现在,我们要完成公理化的第二步了,那就是给合法的项指定变换规则,
在(组合子逻辑中)中,我们称之为weak reduction,即我们令,
(1),可以变换为,
(2),可以变换为,
(3),可以变换为。
如果经过有限步weak reduction转换为,就写为。
与项的范式一样,我们将不能再继续进行weak reduction的项,称为weak范式(weak normal form)。
我们来看一个例子,
设,来计算,
,因为,
,因为,
,
。
有了合法的项(公理),以及weak reduction(推导规则),
我们就建立了另一个形式系统。
3. 与演算之间的关系
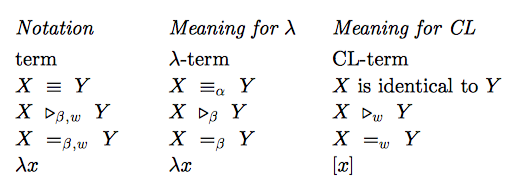
以上我们看到项,似乎只能进行项的应用(application)操作,对应于项的用法为,
然而,其实的威力却不止于此,它的计算能力是与演算相当的。
为了证明等价性,建立项与项之间的关系,
现在我们用,,三个组合子,来定义与相似的概念。
对于任意的项,以及任意的变量,我们定义用如下方式表示,
(1),如果中不含有,
(2),
(3),如果中不含有,
(4),如果(1)和(3)都不适用的话。
例如,
可见,可以完全用,,三个组合子来构建出来,
它表示了与相对应的概念。
因此,我们可以建立项与项的对应关系了,
在中,,相当于演算中,,可以统一记为
,相当于,可以统一记为。
相应的,,,也可以使用项来表示,
,,。
4. 不动点定理
在演算和中,存在组合子,使得。
证明:令,,则,
。
总结
本文我们用公理化的方法,创建了另一个形式系统,
接着,我们发现实际上是与等价的。
可悲的是,知道演算的人很多,但是知道(组合子逻辑)的人却很少,这简直是不可思议的。
下文中,我们将继续沿着公理化和形式系统的道路向前走,敲开数理逻辑的大门。