Algebraic Effects 是什么鬼

发表于 | 分类于

背景

React 16.8.0开始已经支持 Hooks了，

传言 Hooks 受到了Algebraic Effects的启发，

毕竟React团队有不少OCaml开发者。


OCaml with support for (unchecked) algebraic effects and handlers.

Effects and handlers provide concurrency and compose part of Multicore OCaml.

—— Algebraic Effects and Handlers


以下我将algebraic effects当做专题来进行了调研，其中涉及了很多能力之外的知识，

因此，出现理解上的错误是不可避免的。

就当是阶段性的总结吧，读者还请注意分辨，茶余饭后止增笑耳。

1. delimited continuation

但是究竟什么是Algebraic Effects，查了很多资料都没找到答案，

Sam Galson有一篇文章Continuations, coroutines, fibers, effects从JS的角度介绍了react的理论基础，

里面提到了Delimited Continuation，它可用来实现各种effects。



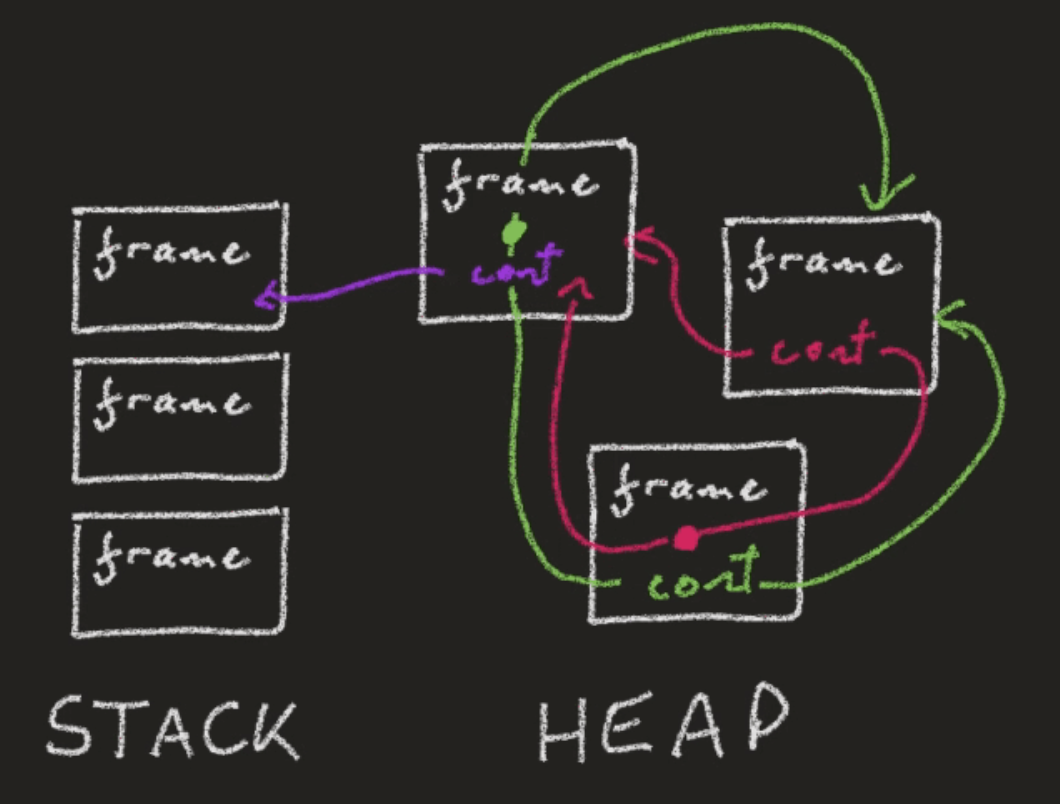
其中Continuation应该是一个很熟悉的概念了，

current continuation（当前位置的continuation）表示程序从某个位置开始，之后到程序结束所有后续的计算，

Scheme中的call/cc就可以用来获取当前位置的 continuation。


至于Delimited Continuation则表示“有界的” continuation，它需要两个操作符，

例如在Racket中，它们是reset和shift，

（1）shift用来捕获当前位置的continuation

（2）reset用来表示shift生效的时间范围（调用顺序）


1
2
3
4
5
6
7
(* 2 
  (reset 
    (+ 1 
      (shift k (k 5))
    )
  )
)

以上代码中，shift捕获了当前位置的continuation，并绑定到k上，

这个continuation是以reset开始调用时未界限的，即，这个continuation可以表示为(+ 1 [*])，

其中的*为continuation中待填充的值。


后面的* 2在reset调用之前，因此不包含在shift捕获的continuation中。

这种截止到reset为止的continuation，就是delimited continuation。


下面我们来看下执行逻辑，

（1）shift中直接调用了(k 5)，它会调用continuation，

（2）最后shift的返回值将作为reset的值。


所以，以上代码相当于，

1
2
3
(* 2 
  (+ 1 5)
)

更多例子，可参考Delimited Continuation，

与一般的Continuation（undelimited continuation）不同的是，

delimited continuation可以看做是一个函数调用，它是有返回值的。


多个shift的场景，k里面又有shift，

第二个shift返回并不会导致reset结束，

1
2
3
4
5
(reset
   (begin
     (shift k (cons 1 (k (void))))
     (shift k (cons 2 (k (void))))
     null))

2. 模拟 generator

有了delimited continuation我们就可以实现很多常见的effects了，

包括IO操作，yield，try/catch等等，


下面直接引用这篇文章中的例子，Continuations, coroutines, fibers, effects

1
2
3
4
5
6
7
8
9
const octuple = n =>
  reset(() => {
    const continueWith = shift(cont => {
      const doubled = cont(n);
      const quadrupled = cont(doubled);
      return cont(quadrupled);
    });
    return continueWith * 2;
  });


其中shift中的cont，表示从shift开始截止到reset为止的delimited continuation，即，

1
x => x * 2

并且shift中对cont调用了好几次，shift的返回值将作为reset的值。

因此，return continueWith * 2;是当做cont执行的，而不是执行完shift再return continueWith * 2;。

shift中return cont(quadrupled);的时候，reset就返回了。


有了delimited continuation我们就可以事先generator了，

1
2
3
4
5
6
const getAddressByUsername = username =>
  reset(() => {
    const userId = shift(getUserId.bind(username));
    const address = shift(getUserAddressById.bind(userId));
    /* continue with address */
  });

其中getUserId中会调用cont，而这个cont则是，

1
2
3
4
userId => {
    const address = shift(getUserAddressById.bind(userId));
    /* continue with address */
}

所以调用cont的时候，会导致第二个shift执行，

第二个shift又产生一个新的cont，表示第二个shift之后的continuation。


我们看到有了delimited continuation，很多复杂的控制结构都可以用它来实现了，

甚至try/catch都可以。


通过改写shift的写法，我们将它放到reset尾部，

1
2
3
4
5
6
7
onst hello = () =>
  reset(() => {
    const continueWith = shift()
    return continueWith + 'world';
  }, cont => {
    return cont('hello');
  });


然后将reset改成handle，将shift改成effect，

并且为了区分其他的handle调用，把effect写为handle的形参。


1
2
3
4
5
6
7
const hello = () =>
  handle((effect) => {
    const continueWith = effect(false)
    return continueWith + 'world';
  }, (isShy, cont) => {
    return isShy ? cont('goodbye') : cont('hello');
  });

3. algebraic? effects?

但是，为什么shift是一种effect呢？

这个effect为什么又是algebraic的呢？


要揭开这个谜题还得去啃论文了。

3.1 model effects

首先在Algebraic Effects for Functional Programming中，作者Daan Leijen提到，

Algebraic effect handlers, are recently gaining in popularity as a purely functional approach to modeling effects.

In this article, we give an end-to-end overview of practical algebraic effects in the context of a compiled implementation in the Koka language.


所以，algebraic effect handlers是一种model（建模） effect的方式。

作者在Koka语言中，实践了一把algebraic effects。


后文作者还说，

Algebraic effects (introduced by Plotkin and Power in 2002 [34]) and algebraic effect handlers (introduced by Plotkin and Pretnar in 2009 [33]), are recently gaining in popularity as a purely functional approach to modeling effects.


因此，引文[34]中肯定提到了Algebraic effects和algebraic effect handlers，

他们都是建模effect的手段。

3.2 computational λ-calculus

我们找到了这篇文献，Algebraic Operations and Generic Effects，作者Gordon Plotkin and John Power是这么说的，

Eugenio Moggi, in [13, 15], introduced the idea of giving a unified category theoretic semantics for computational effects, ...

Examples of such effects are: nondeterminism, probabilistic nonde-terminism, exceptions, interactive input/output, side-effects, and continuations with, ...


作者说Eugenio Moggi从category theory出发，给computational effects提供了统一的语义（这个理论模型叫computational λ-calculus），

这些effects可以涵盖 nondeterminism, probabilistic nonde-terminism, exceptions, interactive input/output, side-effects, and continuations，这么多场景。

也就是这些东西可以用统一的框架来解释。


作者还说，Eugenio Moggi发明的computational λ-calculus其实跟类型化 λ-calculus差不多，

The computational λ-calculus is essentially the same as the simply typed λ-calculus except for making a careful systematic distinction between computations and values.

唯一不同的是，computational λ-calculus严格区分的values和computations。


However, the calculus does not contain operations, the constructs that actually create the effects.

不过computational λ-calculus也有缺陷，它不包含operations。

而所谓operations，就是那些可以产生effects的东西。


但是，Eugenio Moggi还是很强的，虽然computational λ-calculus不包含operations，但是computational metalanguage包含了，

Moggi’s computational metalanguage does contain operations, and his paper [14] includes semantics for them, but he only demanded naturality of the operations in C, and he did not develop a body of theory in support of that semantics. Here, by demanding the stronger coherence condition of parametrised naturality in CT ,

we provide a notion of algebraic operations, which we support by equivalence theorems to indicate definitiveness of the axioms, and which are further supported by our development of a unified operational semantics in [20].

只是语义方面，Eugenio Moggi做的还不够。


因此，作者发明了一个概念称为algebraic operations，来在语义层面进行统一。

所谓，algebraic operations，说白了不过是，

Algebraic operations are, in the sense we shall make precise, a natural generalisation, from Set to an arbitrary symmetric monoidal V-category C with cotensors, of the usual operations of universal algebra, taking T to be a strong V-monad on C.


当然新概念总是会有定义的，


所以，algebraic operations主要还是从语义角度来看的。

它给computational λ-calculus扩充了operation，还给这些operation选了一个catetory theory的语义。


至于computational λ-calculus的细节，可以查阅这几篇，

Notions of computation and monads

Computational Lambda-Calculus and Monads

An Abstract View of Programming Languages

3.3 operations vs effects

以上提到了computational effects，algebraic operation，

怎么就变成algebraic effects了呢？


这个名词来自这篇文献，Adequacy for Algebraic Effects，它是上一篇文献的引文，作者还是Gordon Plotkin and John Power

Moggi proposed a monadic account of computational effects. He also presented the computational λ-calculus ... a core call-by-value functional programming language for effects; the effects are obtained by adding appropriate operations.

嗯嗯，跟我们理解的一致。


The question arises as to whether one can give a corresponding treatment of operational semantics.

In this paper we give such a treatment in the case of algebraic effects where the operations are given by a single-sorted algebraic signature Σ; semantically such an n-ary operation f is taken to denote a family of morphisms fx : T(x) n −→ T(x) parametrically natural with respect to morphisms in the Kleisli category C T ; T is then said to support the family f x .


这里它把operation的语法用single-sorted sigma代数来描述，

而这些operation的语义用category进行解释。


所以，operation是一个语法概念，effects是语义概念。

从 An Introduction to Algebraic Effects and Handlers这篇文献中我们可以看出来，


Algebraic effects are an approach to computational effects based on a premise that impure behaviour arises from a set of operations such as get & set for mutable store, read & print for interactive input & output, or raise for exceptions [16,18].

This naturally gives rise to handlers not only of exceptions, but of any other effect, yielding a novel concept that, amongst others, can capture stream redirection, backtracking, co-operative multi-threading, and delimited continuations [21,22,5].


原来加入到computational λ-calculus中的operation，初衷是为了表示effects，

并且其语义还是algebraic的，所以，称为algebraic effects还是挺合适的，

只不过algebraic太笼统了，容易让人产生其他联系。

把algebraic effects理解为algebraic operation的定义可能更好一些。

3.4 handler

这篇文章An Introduction to Algebraic Effects and Handlers中介绍了algebraic effects handler的用法，

加上handler之后，就和delimited continuation的概念串起来了。

后文还介绍了用delimited continuation实现各种effects的方法，

例如，对于input/output


对于exception，


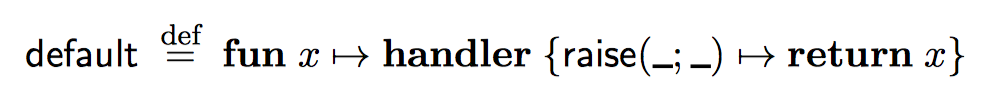
对于non-determinism


还有好多，毕竟computational λ-calculus中的operation就是为了建模各种effects的。

出自Notions of computation and monads

结语

  1. λ calculus 只建模了values不包含computaion。
  2. Eugenio Moggi发明了computational λ-calculus基于category theory建模了values和computation。
  3. 作为扩展Gordon Plotkin and John Power为computational λ-calculus增加了operation用来建模effect。
  4. operation的语法用a single-sorted algebraic signature Σ表示，语义用a family of morphisms（algebraic operation）表示。
  5. 由于operation可以表示effect，所以这样的algebraic operation，又称为algebraic effects。
  6. nondeterminism, probabilistic nonde-terminism, exceptions, interactive input/output, side-effects, and continuations 都是effects。
  7. 它们都可以用delimited continuation实现。


暂且这么理解吧，中间肯定会有很多理解不当之处，

因为我个人也不是学习这个方向的，所以阅读者还请多多见谅，

有专业人士路过的话，请不吝指正。

参考

React 16.8.0

Hooks

github: reactjs/rfcs

OCaml: Concurrent Programming with Effect Handlers

Multicore OCaml

Algebraic Effects and Handlers

Continuations, coroutines, fibers, effects

Delimited Continuation

Continuation


Algebraic Effects for Functional Programming

Algebraic Operations and Generic Effects

Notions of computation and monads

Computational Lambda-Calculus and Monads

An Abstract View of Programming Languages

Adequacy for Algebraic Effects

An Introduction to Algebraic Effects and Handlers