
回顾
上文我们介绍了笛卡尔闭范畴,它给出了简单类型化演算系统的语义,
我们还看到了笛卡尔闭范畴与柯里化之间的关系。
结合《你好,类型》系列文章,
到目前为止我们已经有了,类型理论,逻辑学和范畴论的知识基础了。
现在我们介绍Curry-Howard-Lambek correspondence,将三者联系起来。
1. 类型方面

我们来回顾一下简单类型化演算系统。
1.1 语法
例子:
1.2 类型
基本类型(basic types),
一般类型(general types),
例子:
,
1.3 类型推导规则
(1)
(2),,
(3),
其中,,。
2. 逻辑方面
参考《你好,类型(四):Propositional logic》,
我们构建一个只包含逻辑联接词和的命题逻辑系统。
2.1 逻辑推导规则
(1)
(2),,
(3),
2.2 Curry-Howard correspondence
我们看到,只要将逻辑系统中的和,替换成简单类型化演算中的和,
那么这两个系统从推导规则上来看是一致的。
逻辑中的命题,对应了简单类型化演算中的类型,
逻辑中命题的证明,对应了简单类型化演算中的项(的类型断言)。
命题,可以这样理解,
如果该命题可证,则存在将的证明转换为的证明的构建过程(construction)。
命题,可以这样理解,它是和的证明序对(pair)。
考虑到以上命题逻辑与类型之间的对应关系,
我们可以说,proofs as programs。
3. 范畴论方面
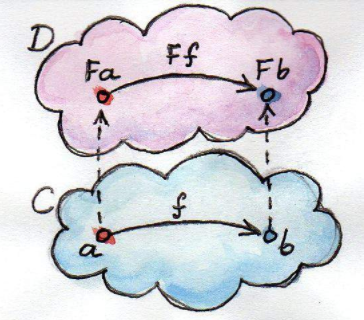
结合《语言背后的代数学(九):笛卡尔闭范畴》,
我们给出了简单类型化演算的范畴论解释。
3.1 对象
将简单类型化演算系统的类型,解释为笛卡尔闭范畴中的对象。
3.2 箭头
将带有自变量项,解释为从自变量类型到项类型的箭头。
3.3 Curry-Howard-Lambek correspondance
根据简单类型化演算系统中的推导规则,
我们可以为范畴添加对象和箭头之间的约束条件,
(1)
(2),,
(3),
是一个箭头,和的定义,
可以参考前一篇文章中关于笛卡尔闭范畴的定义。
笛卡尔闭范畴作为简单类型化演算系统的语义模型,
范畴中箭头之间约束关系,与类型推导规则是一致的,
而根据Curry-Howard correspondence,类型推导规则与命题逻辑又是一致的。
因此,类型理论,逻辑学和范畴论产生了关联,
这种三者的对应关系,称为Curry-Howard-Lambek correspondance。
总结

本文介绍了Curry-Howard-Lambek correspondance,
它将本来毫无关系的三个学科联系在了一起,
类型理论与程序和计算相关,逻辑学与证明(论)相关,
范畴论与模型(论)和代数学相关。
本系列文章到此结束了,与代数学和范畴论相关的内容其实还有很多,
例如,quotient algebra,comonad,adjoint functor,free monoid,等等概念,
书山有路勤为径,学海无涯苦作舟,让我们一起努力吧。
参考
Curry-Howard-Lambek correspondence
The Curry-Howard Correspondence, and beyond