回顾
上文我们简单的介绍了一些范畴论相关的内容，
范畴由一些对象和箭头组成，范畴之间的箭头称为函子，
函子之间的一族箭头称为自然变换。
范畴的对象不一定是集合，所有的箭头也不一定构成一个集合。
如果一个范畴，它的对象都是集合，所有的箭头也构成了一个集合，
就称该范畴是一个小范畴（small categories）。
1. 定义域和值域
在集合论中，函数自变量所有可取值的集合，称为函数的定义域，
给定函数，其中就是的定义域，记为，
集合，称为的值域，记为。
在范畴论中，箭头也有定义域和值域的概念。
箭头，表示了对象和之间的关系，
我们称为箭头的定义域（domain），记为，
为箭头的值域（codomain），记为。
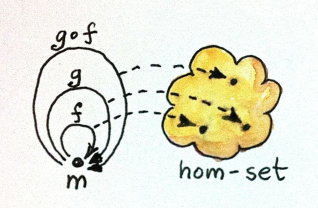
由此，我们还可以定义范畴中，从对象到对象所有箭头的集合，
，常被称为hom-set。
2. 笛卡尔闭范畴
笛卡尔闭范畴是一种带有附加结构的范畴，这个名字虽然不是那么熟悉，
而实际上，我们经常遇到它。
2.1 笛卡尔积
两个集合和的笛卡尔积，是以下所有可能有序对构成的集合，
。
2.2 笛卡尔积上的函数
，是从笛卡尔积到的函数，
我们可以用两种不同的视角来看待它，
（1）它是一个一元函数，参数取遍中的所有元素。
（2）它是一个二元函数，一个参数来自于，另一个来自于。
原则上，这两种理解应该是不同的，然而它们却是等价的。
2.3 柯里化
笛卡尔闭范畴就是反映这一类性质的数学结构，
一个范畴中，定义在乘积对象上的箭头，
总是可以“自然的”由定义在某一个对象或上的箭头来决定。
这就是柯里化（curring）的概念，
将一个二元函数柯里化指的是，将它看成一个一元函数，
这个函数返回另一个一元函数。
假设是一个函数，
令是所有到的函数，
则存在唯一的，使得，。
函数称为的柯里化。
用hom-set的术语来表述就是，存在一个一一映射，使得，
2.4 Cartesian Closed
将以上柯里化的概念推广到范畴论中，我们就有，
一个笛卡尔闭范畴（cartesian closed category），是满足以下几个额外条件的范畴。
（1）中存在一个对象，使得对于任意对象，有唯一的箭头，
这样的对象，称为终对象（terminal object）。
（2）对于任意两个对象和，范畴中存在一个对象，
以及两个箭头和，使得，，。
（3）对于任意两个对象和，
范畴中存在一个对象，以及一个箭头，使得，
对于任意的箭头，存在唯一的箭头，
有恒成立。
即，。
其中，为对象的恒等箭头，称为指数对象（exponential object）。
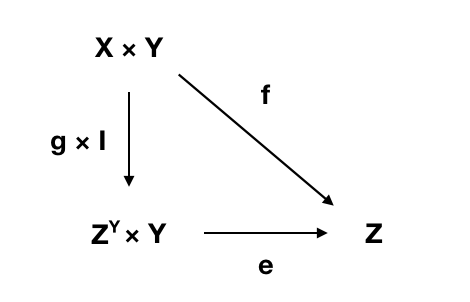
3. 项的解释
在第六篇中，为了解释简单类型化演算，
我们为每一个项，找到了一个代数中数学对象与之对应，
简要的说，我们用代数的载体来解释基本类型，
用载体上的函数集来解释类型为的所有函数。
现在有了笛卡尔闭范畴，我们准备为每一个基本类型选择范畴中的一个对象，
而将项常量解释为范畴中的一个箭头（原因在下文解释），
其中为我们在Henkin模型中定义的含义函数。
3.1 封闭项的解释
我们这样定义一个含义函数，
（1）
（2）
（3）
（4）
3.2 带有自由变量的项
如果是一个含有自由变量的项，
则在笛卡尔闭范畴中，它应该解释为从自由变量的语义对象到的语义对象的一个箭头，
。
值得一提的是，
这里说明了，项常量为什么不能被解释为范畴中的对象，
而是解释成了箭头。
其中，类型上下文的解释，定义如下，
（1）
（2）
回顾
本文介绍了笛卡尔闭范畴，是一种具有特殊结构的范畴，
它补充了柯里化这一概念所需满足的约束条件。
接着我们用笛卡尔闭范畴解释了，
带有单位类型，乘积类型的简单类型化演算。
参考
你好，类型（六）：Simply typed lambda calculus