
回顾
上文中,我们用群,拓扑空间,CPO作为例子,
来说明什么是数学结构,以及数学结构是如何通过映射来保持的。
群同态保持了群结构,连续映射保持了拓扑结构,
连续函数保持了完全偏序结构。
那么群结构与拓扑结构之间是否有联系呢?
我们能否建立拓扑空间与群之间的对应关系呢?
在代数拓扑中,就存在这样的例子,
人们找到了和拓扑空间相关的群论概念,例如基本群和同调群,
拓扑空间的连续映射可以导出这些群的群同态。
这就为了人们使用代数学方法研究其他数学分支,奠定了基础,
实际上,最原始的范畴论想法也是起源于此。
1. 图示法
在前一篇中我们学过了幺半群,
它指的是一个集合,以及上的二元运算,满足以下两个条件,
(1),,
(2),,。
这两个条件除了可以用等式来表示,还可以用图(diagram)来表示,
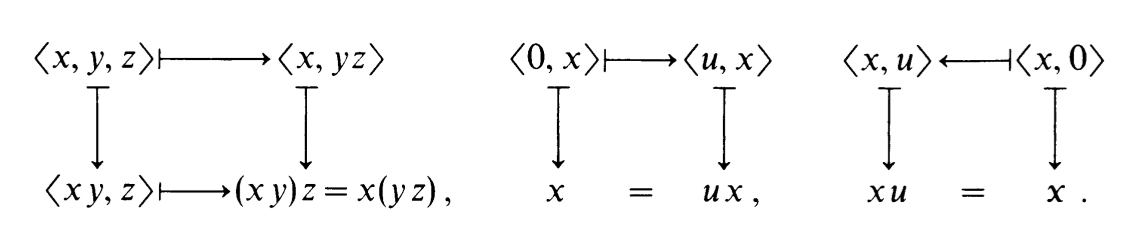
我们称以上两张图都是可交换的(commutative),
即,沿着不同的路径进行运算,只要起点和终点相同,则运算的结果就相同。
例如,,
总是等于,
即,,表明中元素的运算满足结合律。
又例,,总是等于,即,
,总是等于,即。
因此,,表明中存在幺元。
所以,我们可以用以上两个图表,作为幺半群的定义,称为图示法。
另一方面,考虑在集合论中讨论映射的时候,一般都不写具体元素,还可以表示为,
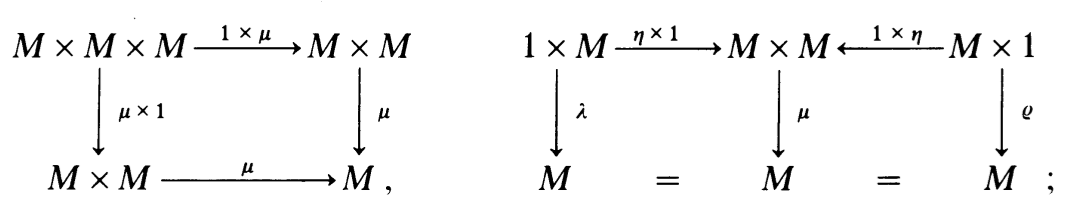
其中,,,是两个函数,
是只有一个元素的集合。
用图示法来表示幺半群,更具一般性。
2. 范畴
范畴是一个数学概念,也可以用图示法来表示。
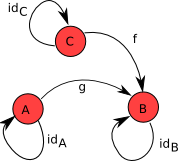
一个范畴由一系列对象(object)和箭头(arrow)组成。
对于每一个箭头,有两个对象与之关联,
称为箭头的定义域(domain)和值域(codomain)。
并且,还要满足以下几条规则,
(1)对于每一个对象,存在恒等箭头(identity arrow),
(2)箭头满足结合律,对于任意的箭头,有
(3)箭头的集合在箭头组合运算下是封闭的
其中,表示和的组合运算,
它也是一个箭头,其中的值域是的定义域。
例子:
所有的集合,以集合为对象,集合之间的映射作为箭头,构成了一个范畴,
所有的群,以群作为对象,群同态作为箭头,构成了一个范畴,
所有的拓扑空间,以拓扑空间作为对象,拓扑空间之间的连续映射为箭头,构成了一个范畴。
以上三个例子中,
范畴中的对象都是集合,箭头都是映射,这就很容易造成误解。
因为,范畴中的对象可以不是集合,箭头也可以不是映射,
理解这一点至关重要。
例如,完全偏序,
以中的元素作为对象,以作为之间的箭头,同样构成了一个范畴。
3. 函子
函子就是两个范畴之间的箭头。
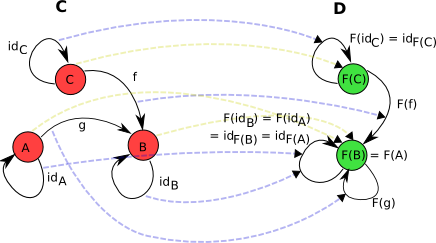
一个函子是范畴到范畴的箭头,,它满足以下条件,
把中的对象映射为中的对象,把中的箭头映射为中的箭头。
并且,。
值得注意的是,
等式左边的,表示中的箭头组合运算,
等式右边的,表示中的箭头组合运算。
4. 自然变换
自然变换(natural transformation)是一族箭头,
将范畴在一个函子中的像(picture),变换成了另一个函子的像。
给定两个函子,其中和是范畴。
自然变换的每个分量(components)使下图可交换。
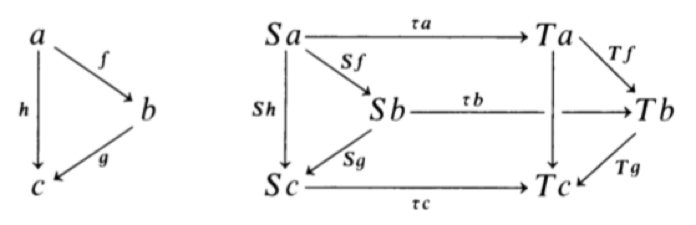
其中,是中的箭头,。
5. Monad
范畴到自身的函子,称为自函子(endofunctor)。
设是任意范畴上的自函子,自函子复合之后仍为自函子,
,。
令是一个自然变换,其分量为,,
则使用可以定义另外两个自然变换,
,它的分量为,
,它的分量为。
范畴上的一个Monad,指的是三元组,
它们使下图可交换,
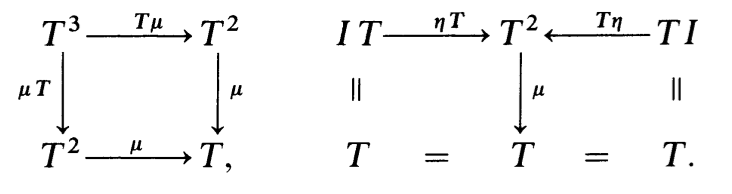
其中,是范畴上的自函子,
,是两个自然变换。
值得注意的是,Monad与幺半群的图示法是相似的,
只需要将幺半群定义中的,改写成自函子的复合运算,
把单位集合,改写成单位自函子即可。
因此,我们说Monad是自函子范畴上的一个幺半群。
All told, a monad in X is just a monoid in the category of endofunctors of X, with product x replaced by composition of endofunctors and unit set by the identity endofunctor.
6. Hask范畴上的Monad
如果把Haskell语言中的类型作为对象,把类型之间的函数看做箭头,
则在函数复合运算下,构成了一个范畴,称为Hask范畴。
函子
Haskell中类型类(type class)Functor的每一个实例,
定义了Hask范畴中的一个函子。
1 | class Functor (f :: * -> *) where |
fmap表示了函子作用在箭头上的结果。
作用在对象上,可以使用pure :: a -> f a来表示。
在Haskell中,一个类型要成为Functor的实例,
还要满足相应的“Functor Law”,
1 | fmap id = id |
可以证明,
这些“Functor Law”刚好使f,fmap和pure构成了范畴论意义上的函子。
Monad
Haskell中类型类Monad的每一个实例,
定义了Hask范畴中的一个Monad。
1 | class Functor m => Monad m where |
在Haskell中,一个类型要成为Monad的实例,
还要满足相应的“Monad Law”,
1 | return a >>= k = k a |
可以证明,
这些“Monad Law”刚好使m,>>=和return构成了范畴论意义上的Monad。
总结
本文介绍了范畴论相关的一些内容,
介绍了什么是范畴,什么是函子,什么是自然变换,
这些都是理解笛卡尔闭范畴所必须的。
为了理解什么是范畴,我们列举了前一篇提到的群,拓扑空间,CPO作为例子,
还借用了Haskell中的Functor和Monad学习了Hask范畴。
下文我们将继续学习范畴论,
理解什么是笛卡尔闭范畴,以及如何用它解释简单类型演算的语义。