
回顾
上文中我们介绍了一个称为“pq”的系统,
并且给它选择了一个合理的语义解释。
我们将---q-p--解释为“3等于1加2”。
此外,我们还知道了,
解释的方式,是随着形式系统的公理化条件而改变的。
更改了“pq系统”的公理或者推导规则的时候,
系统中公理和定理的含义都会发生改变。
为此我们回顾了几何学中的欧几里得第五公设问题,
看到了语义问题对数学家们造成的困扰。
自然数语言
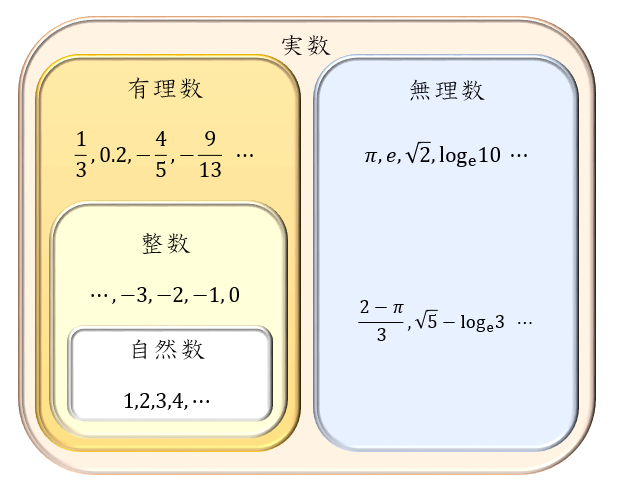
从读小学的时候开始,我们就认识了自然数,
我们可以从零开始计数,每个数字比它前面的多一,
这些数字可以用来表示物品的个数。
它们是如此的贴近生活,如此自然,
以致我们一直以来,就把两个不同的概念混淆在了一起。
一个概念是自然数的语法构造,属于编码问题,
另一个概念则是对这种语法构造的解释,属于语义问题。
为了看清这一点,
我们使用公理化方式定义一个自然数形式系统。
为此我们要问自己这些问题。
(1)这个形式系统包含了哪些符号呢?
它只包含0~9,这个十个字符。
(2)哪些符号串是合法的?
一位符号串,或者不是0开头的多位符号串,都是合法的。
所有这些合法的符号串,构成了一个集合,称为该形式系统的“语言”。
(3)哪些符号串被认为是公理或定理,定理之间的推导规则是什么?
对于自然数形式系统来说,符号串0可以看做公理,后继函数可以看做推导规则。
(4)这些符号串的含义是什么?
简单起见,我们可以直接指定符号串的含义为它所对应的那个自然数。
例如,3是一个符号串,我们指定它对应这个自然数。
其中3是语法符号,是数学对象。
Peano系统
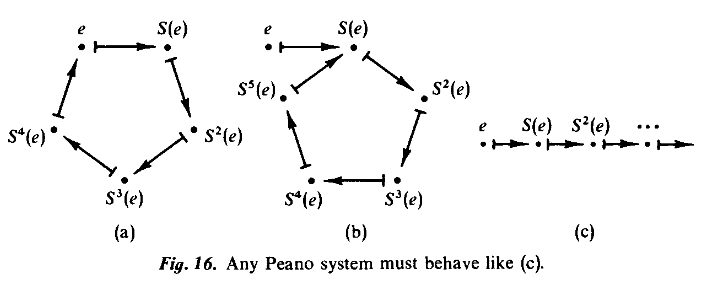
上一节我们使用公理化的方式建立了一个形式系统,
并且选择了自然数作为该形式系统中符号串的解释。
可是在数学上,自然数到底是什么呢?
要回答这个问题,
皮亚诺(Peano)将自然数理论建立在了集合论之上。
其中,构成了一个归纳集。
我们将定义为自然数,(von Neumann construction)
每一个自然数就和一个集合对应起来了。
因此,自然数是一个集合,
,
其中,为集合的后继运算,。
总而言之,符号串3的数学解释,
是一个集合。
(不必惊讶。
自然数代数

在读小学的时候,数学课只有一门,主要学有理数的四则运算,
而到了初中,数学就变成了两门,分为代数课与几何课,
代数课主要讲方程和函数,几何课主要讲平面几何。
平面几何是很直观的,也很容易和其他数学划清界线,
因此,初中生们对“什么是几何”都没有太多疑惑。
但是至于“什么是代数”,就比较费解了,这个问题也困扰了我很久。
到大学,我们又学了线性代数,这种困扰日益加深,
因为居然出现了一种“线性的”“代数”,
却没有人事先告诉我们到底什么是“代数”。
后来我们学了抽象代数,这个问题才得以解决,
我找到了一个令自己满意的答案。
为了说明“什么是代数”,最简单的办法就是下定义,
设集合上定义了一组运算,,
运算结果仍是中的元素,则称相对于这个运算,构成了一个代数。
一般来说,代数问题的特点,
是对一类问题,利用统一的运算性质,求出所有可能的解答。
因此,代数学就是研究运算系统性质的学问。
而Peano系统,是最简单的运算系统之一,又称为一阶算术系统。
自然数就是这个系统中的运算对象。
因此,小学数学也称为“算术”。
代数学观点
随着代数学的发展,人们发明了许多运算系统,
例如,整数的加减法,有理数的四则运算,实数的根式或指数运算,等等。
它们都有现实的对应物,仿佛数学的研究对象就是现实世界一样。
然而,实际上并非如此。
例如,复数,它是没有现实对应的,
但是我们仍然可以对复数进行运算。
一个次方程可能在实数范围内无解,但必定会存在个复数解。
引入了复数之后,我们也才能体会到欧拉公式之美,
另一方面,代数学的研究重点也发生了改变,
一开始人们研究的是单个的,独立的,具体的运算系统,
但是后来人们逐渐发现,很多运算系统有相同的运算性质,
可以抽象出来进行讨论。
例如,计算机系统中的无符号数,连同加法运算,构成了一个阿贝尔群。
而阿贝尔群中的加法,满足交换律和结合律,
因此,编译器就可以采用任意的顺序进行计算,不影响最终结果。
从运算性质的角度来分析问题,越来越流行了,
成为了现代数学不可或缺的一部分,
并且,代数学考虑问题的方法,也逐渐影响着其他学科。
总结
本文从语义和代数学角度重新认识了自然数,
自然数是Peano系统中的运算对象,
自然数集连同其上定义的后继运算,构成了一个代数(一阶算术系统)。
更重要的是,从代数学角度来看待问题,
有利于我们抓住系统中所隐含的运算性质。