
1. 初窥语义
在《你好,类型》系列中,我们介绍了一些形式系统,
例如系统(演算),(组合子逻辑),
它们由一些合法的符号,以及这些符号的推导规则构成,
命题逻辑与谓词逻辑,也可以用这种公理化的方式构建起来。
然而,在讨论这些系统的时候,我们只是把它们看成了单纯的符号演算,
并没有过多考虑这些符号到底代表什么含义。
例如,项,经过变换,
我们可以得到,,
。
它看起来真的好像一个函数调用啊。
这就给我们带来了以下思考,
是否可以把解释为一个函数呢?
1 | function (x){ |
是否可以认为,是用参数对该函数进行调用呢?
1 | (function (x){ |
这样解释的话,变换就可以看做函数调用了。
这一切似乎顺理成章,显而易见。
可是,我们为什么可以这样做呢?
变换与函数调用之间的关系是唯一确定的吗?
为了回答好这些问题,还得重新研读语义学这个有趣的学科。
2. 公理化

首先我们先回顾一下,
形式系统是怎么用公理化的方式构建的。
我们以一个称之为“pq”的系统为例。
(出自《哥德尔、艾舍尔、巴赫——集异璧之大成》)
2.1 公理化步骤
第一步,
我们要有一些符号。
例如:“pq系统”只有三个符号,p,q,-。
第二步,
我们要说明什么样的符号串是合法的,即指定一套语法。
例如,我们规定“pq系统”中合法的符号串,形如xqypz,
其中,x,y,z仅由一串短杠组成。
1 | term := n 'q' n 'p' n |
因此,--q-p-,---q--p-都是合法的符号串。
第三步,
我们要指定公理和推导规则,
其中公理是推导的出发点,由公理推导得出的符号串称为定理。
(1)“pq”系统的公理如下,
只要x仅由一串短杠组成,那么x-qxp-就是一条公理。
(2)“pq”系统的推导规则是这样的,
假设x,y和z都代表只包含短杠的特定的符号串,
并且假设xqypz是一条已知的公理/定理,
那么x-qypz-就是一条定理。
即它们满足,表示如果是定理,则也是定理。
例子,根据公理的定义,我们知道--q-p-是一条公理,
又根据这条公理和推导规则,我们得到了---q-p--是一条定理。
小结:
以上三步我们通过公理化的方式构建了一个形式系统,
它由符号,语法,公理,推导规则组成,
我们可以用公理和旧定理生成新定理,不断演算。
在其他系统中,公理和定理的个数可能是有限的,
而“pq”系统则是无限的。
2.2 解释

我们说以上“pq系统”定义了一个形式语言,
这里的“语言”是一种数学上的定义,指的是字符串的集合。
“pq”系统的形式语言,
就是系统中公理和定理的集合。
考察一个形式语言,通常我们要研究它的两个方面,
其一,形式语言的语法,指的是字符串的构成方式,
其二,形式语言的语义,指的是每个字符串的含义。
我想大家都已经读过《计算机程序的构造与解释》了吧,
所谓构造,指的就是语法,而解释指的就是语义。
那我们来看一看“pq系统”的形式语言该怎样解释吧。
我们可以选择这样的解释方式,
例如,我们可以将q解释为“等于”,而将p解释为“加”,
将短杠解释为数字。
于是,---q-p--就可以被解释为“3等于1加2”了。
值得注意的是,合理的解释并不一定是唯一的,
例如,我们将q解释为“减”,将p解释为“等于”,也是可以的。
3. 重新解释

上文中我们先给出了形式系统,
然后再为系统选择一个合理的解释,
这种思维过程是值得提倡的。
考虑语义问题的时候,
我们应该总是先想想,当前在对什么系统进行解释。
例如,对“pq”系统,我们再引入一条新的公理,
新公理:
只要x仅由一串短杠组成,那么xqxp-也是一条公理。
现在来看,引入的新公理对“pq系统”产生了什么影响。
首先,-q-p-在新系统中是一条公理,而在老系统中不是。
其次,根据推导规则,--q-p--是新系统中的一条定理,而在老系统中也不是。
考虑到我们之前对符号串的解释,我们发现,
如果仍然沿用老系统对符号串的解释,
--q-p--应该被解释为“2等于1加2”,
这显然是不正确的。
因此,在系统发生变化的时候,旧的解释可能就行不通了,
我们要对系统选择一个新的解释。
例如,我们只需要将q解释为“小于或等于”就行了。
然而,现在看来这种顺利成章的事情,却困扰了数学家们很多年。
这是整个19世纪数学的最深刻的教训之一。
4. 非欧几何
大家应该都听说过欧几里得第五公设的故事,
欧几里得采用了公理化的方式构建了几何学,
其中第五公设又称平行公设,它既不能被其他公设证明,也不能证否,
两千年来,在第五公设问题上,耗费了无数年轻数学家的生命和心血。
如果两条直线与第三条直线相交时,在第三条直线的某一侧三条线所夹的内角之和小于两个直角的和,则那两条直线沿着这一侧延伸足够长之后必然相交
1820年左右,俄国喀山大学教授罗巴切夫斯基,
提出了一个与第五公设相矛盾的命题,
然后与欧几里得的前四个公设结合成一个公理系统,展开一系列的推理。
他认为如果这个系统在推理中出现矛盾,就等于证明了第五公设,
此即数学中的反证法。
但是,在他极为细致深入的推理过程中,
得出了一个又一个在直觉上匪夷所思,
但在逻辑上毫无矛盾的命题。
这在当时是一件很难理解的事情,
因为人们一致认为,欧几里得几何是物质空间中图形性质的正确理想化。
正确的几何结论不应该与我们的直观感受不符。
现在看来,这样理解当然是有问题的,
因为,它混淆了公理系统中的结论,和对这些结论的解释。
就好像上文中我们为“pq”系统增加了新公理一样,
新定理仍然是正确推导的产物,只是不能沿用旧方式进行解释了。
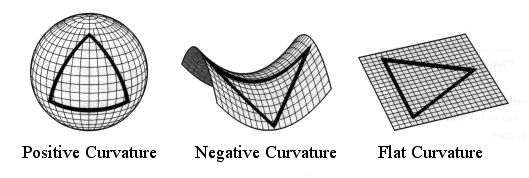
关于欧几里得第五公设,最终人们得到了三种常用的几何学,
称为欧几里得几何,罗巴切夫斯基几何,以及黎曼几何。
这些公理系统,对研究不同的数学对象起到了关键作用。
5. 总结
本文通过一个称之为“pq”的系统,介绍了形式系统公理化的典型步骤,
并且严格区分了,公理系统中的结论与对它的解释之间的不同。
通过更改公理系统,不论修改公理或者修改推导规则,我们将得到一个新的系统,
从而对新系统中的结论,我们就得采用审慎的方式重新解释。
这是数学史给我们带来的最有价值的经验教训之一。