
类型变量
到目前为止,我们遇到的每一个项都有唯一确定的类型,
因为,项的类型都被显式的注释在了它的后面。
例如,我们可以定义一个恒等函数,
则的类型就是固定的,,而就不是良类型的。
为每一个类型的恒等函数都定义各自的版本,是非常繁琐的,
因此,一个自然的想法是,我们能否让的类型参数化,
让它在不同的上下文中,实例化为不同的具体类型。
例如,,其中是类型参量。
类型代换
类型代换,指的是一个从类型变量到类型的有限映射。
例如,,会将类型变量分别代换为。
其中,称为代换的定义域,记为,
而称为代换的值域,记为。
值得一提的是,所有的代换都是同时进行的,,
是将映射成,将映射成,而不是。
代换可以用下面的方式来定义,
(1),如果
(2),如果
(3),
(4)
对于类型上下文来说,
类型代换的一个重要特性是它保留了类型声明的有效性,
如果包含类型变量的项是良类型的,那么它的所有代换实例也都是良类型的。
类型推断
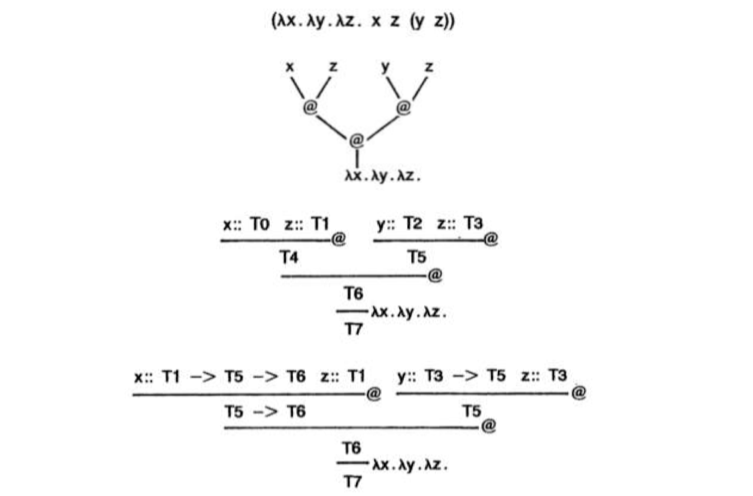
在类型上下文中,对于包含类型变量的项,我们通常会提出两个问题,
(1)它的所有代换实例,是否都是良类型的?
即,是否。
(2)是否存在良类型的代换实例?
即,是否。
对于第一个问题,将引出参数化多态(parametric polymorphism),
例如,,它的类型为,
无论用什么具体类型来代换,代换实例都是良类型的。
对于第二个问题,原始的项可能不是良类型的,
但是可以选择合适的类型代换使之实例化为良类型的项。
例如,,是不可类型化的,
但是如果用代换,用代换,
,
就可以得到,,
可类型化为。
或者,取,结果也能得到一个良类型的项,尽管仍包含变量。
在寻找类型变量有效实例的过程中,出现了类型推断(type inference)的概念。
意味着由编译器来帮助推断项的具体类型,
在ML)语言中,程序员可以忽略所有的类型注释——隐式类型(implicit typing)。
在进行推断的时候,对每一个原始的抽象,
都用新的类型变量进行注释,写成,
然后采取特定的类型推导算法,找到使项通过类型检查的一个最一般化的解。
设为类型上下文,为项,
的解,是指这样的一个序对,使得成立。
例如,设,,则
,,
都是的解。
基于约束的类型化
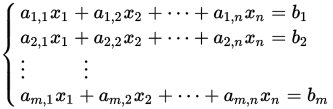
(1)约束集
在实际情况中,的解,并不一定满足其他类型表达式的约束条件,
所以,我们寻找的是满足这些约束条件的特解。
所谓约束条件,实际上指的是约束集,
它由一些包含类型参量的项的等式构成,。
如果一个代换的代换实例,和相同,则称该代换合一(unify)了等式。
如果能合一中的所有等式,则称能合一(unify)或满足(satisfy)。
我们用,来表示约束集满足时,项在下的类型为,
其中为约束集中,所有类型变量的集合,有时为了讨论方便可以省略它。
例如,对于项,
约束集可以写为,则类型为。(算法略)
而代换,
使得等式成立,
所以,我们推断出了是项的一个可能类型。
(2)约束集的解
约束集的解一般不是唯一的,所以一个关键问题是如何确定一个“最好”的解。
我们称代换比更具一般性(more general),如果,记为,
其中,为一个代换,表示代换的复合,。
约束集的主合一子(principal unifier)指的是代换,
它能满足,且对于所有满足的代换,都有。
如果的解,对于任何其他解,都有,
则称是一个主解(principal solution),称为的主类型(principal type)。
可以证明,如果有解,则它必有一个主解。
let多态

多态(polymorphism)指的是单独一段程序能在不同的上下文中实例化为不同的类型。
其中let多态,是由let表达式引入的多态性。
(1)单态性
假设我们定义了一个函数,它能将一个函数对参数应用两次,
此时,的类型为。
如果我们想将应用于其他类型,就必须重写一个新的,
此时的类型为。
我们不能让一个函数,既能用于类型,又能用于类型。
即使在中用类型变量也没有用,
例如,如果写,
则在定义中使用,会产生一个约束,
而在定义中使用,则会产生约束,
这样会使类型变量的求解发生矛盾,导致整个程序不可类型化。
(2)多态性
let多态所做的事情,就是打破这个限制,
让类型参量在上述不同的上下文中,可以分别实例化为和。
这需要改变与let表达式相关的类型推导规则,在第七篇中,我们提到过,
它会首先计算作为的类型,然后再用来确定的类型。
此时,let表达式,可以看做的简写。
为了引入多态性,我们需要对上述类型推导规则进行修改,
它表示,先将中的用代换掉,然后再确定的类型。
这样的话,
就相当于,
通过let多态,产生了的两个副本,并为之分配了不同的类型参量。
此时,let表达式,可以看做的简写。