
上文我们介绍了简单类型化演算系统,并给它扩充了单位类型,
本文继续为它添加新的特性。
我们将提到let和letrec表达式,函数的不动点,
代数数据类型,以及递归类型。
最后我们发现,无类型系统实际上是具有,唯一递归类型的一种情形。
let绑定
当写一个复杂表达式的时候,为了避免重复和增加可读性,
通常我们会给某些子表达式命名,
其中一个常用办法是,使用let表达式。
为此,我们要对简单类型化演算系统进行扩展,
添加let表达式的语法项,求值规则以及类型规则。
新的语法:
新的求值规则:
新的类型规则:
这样我们就可以写出let表达式了,
,
它表示,求值表达式,然后将其绑定到中自由出现的上面,
即在当前这种情况下(顾及let polymorphism),let可以表示为,。
不动点
以上let表达式,,
对求值的时候有一个限制,那就是中不能出现,
否则就像方程一样,出现在了等式的两边,,
此时,中自由出现的,将是这个方程的解。
不过,通常而言,中是可以出现的,
这时候我们就需要使用letrec进行绑定了。
为了看清letrec的真面目,我们用一个求阶乘的例子来说明问题,
其中,表示整数类型。
为了求解,
我们定义一个新函数,使得,
,
注意到,所以是的不动点。
这里我们暂且不讨论不动点的存在性和唯一性问题,
只是引入一个不动点算子,,
它可以用来计算任意函数的不动点。
为了达到这个目的,必须满足以下约束条件,
。
引入了之后,letrec就可以用let表示出来了,
代数数据类型
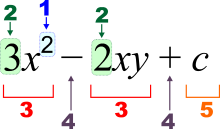
在某些编程语言中,可以自定义递归类型,例如在Haskell中,
1 | data List a = Nil | Cons a (List a) |
以上定义采用了递归的方式,定义了一个代数数据类型List,
所谓代数数据类型,是由基本类型经过复合运算,得来的类型。
Haskell中,使用|表示和类型(sum type),
而带参数值构造器(value constructor)Cons,用于表示各参数(a,List a)类型的积类型(product type),
无参构造器Nil,用来表示单位乘积类型(empty product)。
(关于函数类型与指数的关系,以后有机会再介绍。)
和letrec中的场景相似的是,List也出现在了等式的两边,
于是,我们定义,表示满足等式的最小类型,
其中,和是类型,且通常会在中出现。
因此,以上递归定义的List类型可以表示为,
其中,表示类型参数a,
是一个函数,用于表示类型构造器(data constructor)List,
算子用来计算类型的不动点。
无类型演算
在无类型演算系统中,
定义递归类型,,它满足类型等式。
这样的话,无类型演算系统,
就可以无缝的嵌入到一个类型化的系统中去了,
该系统只存在一个类型,即递归类型,
所有的项,都具有这个类型。
因此,对于支持递归类型的系统而言,
无类型相当于具有唯一类型(Untyped means uni-typed)。
总结
本文介绍了递归类型,引入了两个算子和,分别用来求解函数和类型的不动点。
但是,待求的不动点是否存在,是否唯一,我们仍不能确定。
要想证明这件事情并不简单,需要补充很多额外的数学知识,例如,良基归纳法和最小不动点定理,
此外,不动点的存在性,和递归的终止性也有关系。
好在我们所遇到的大多数场景,都是满足这些要求的,
因为,我们总是先确信这个解是存在的,然后再去编程,例如,
1 | fact :: Int -> Int |
将fact写到等式两边,能让我们更方便对fact进行定义。