1. Regular Languages
1.1 Definition of a DFA
A deterministic finite automaton consist of:
A finite set of states, often denoted .
A finite set of input symbols, often denoted .
A transition function that takes as arguments a state and an input symbol and return a state. The transition function will commonly be denoted . In our informal graph representation of automata, was represented by arcs between states and the labels on the arcs. If is a state, and is an input symbol, then is that state such that there is an arc labeled from to .
A start state, one of the states in .
A set of final or accepting states . The set is subset of .
A deterministic finite automaton will often be referred to by its acronym: DFA. The most succinct representation of a DFA is a listing of the five components above. In proofs we often talk about a DFA in "five-tuple" notation:
where is the name of the DFA, is its set of states, its input symbols, its transition function, its start state, and its set of accepting states.
1.2 Extended transition function
Now we need to make the notion of the language of a DFA precise. To do so, we define an extended transition function that describes what happens when we start in any state and follow any sequence of inputs. If is our transition function, then the extended transition function constructed from will be called . The extended transition function is a function that takes a state and a string and returns a state -- the state that the automaton reaches when starting in state and processing the sequence of inputs . We define by induction on the length of the input string, as follows:
Basic: . That is, if we are in state and read no inputs, then we are still in state .
Induction: Suppose is a string of form ; that is, is the last symbol of , and is the string consisting of all but the last symbol. For example, is broken into and . Then
1.3 The Pumping Lemma for Regular Languages
Let be a regular language. Then there exists a constants (which depends on ) such that for every string in such that , we can break into three strings, , such that:
For all , the string is also in .
That is, we can always find a nonempty string not too far from the beginning of that can be "pumped"; that is, repeating any number of times, or deleting it (the case ), keeps the resulting string in the language .
Proof: Suppose is regular. Then for some DFA . Suppose has states. Now, consider any string of length or more, say , where and each in an input symbol. For define state to be , where is the transition function of , and is the start state of . That is, is the state is in in after reading the first symbols of . Note that .
By the pigeonhole principle, it is not possible for the different 's for to be distinct, since there are only different states. Thus, we can find two different integers and , with , such that . Now, we can break as follows:
That is, takes us to once; takes us from back to (since is also ), and is the balance of . The relationships among the strings and states are suggested by Figure below. Note that may be empty, in the case that . Also, may be empty if . However, can not be empty, since is strictly less than .
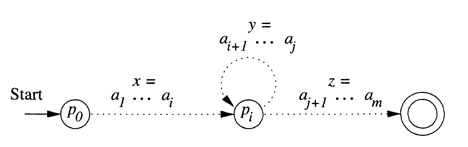
Figure: Every string longer than the number of states must cause a state to repeat.
Now, consider what happens if the automaton receives the input for any . If , then the automaton goes from the start state (which is also ) to on input . Since is also , it must be that goes from to the accepting state shown in Figure above on input . Thus accepts .
If , then goes from to on input , circles from to times on input , and then goes to the accepting state on input . Thus, for any , is also accepted by ; that is, is in .
2. Context-Free Languages
2.1 Definition of Context-Free Grammars
There are four important components in a grammatical description of a language:
There is a finite set of symbols that form the strings of the language being defined. We call this alphabet the terminals, or terminal symbols.
There is a finite set of variables, also called sometimes nonterminals or syntactic categories. Each variable represent a language; i.e., a set of strings.
One of the variables represents the language being defined; it is called the start symbol. Other variables represent auxiliary classes of strings that are used to help define the language of the start symbol.
There is a finite set of productions or rules that represent the recursive definition of a languages. Each production consists of:
A variable that is being (partially) defined by the production. This variable is often called the head of the produciton.
The production symbol .
A string of zero or more terminals and variables. This string, called the body of the production, represents one way to form strings in the languages of the variables of the head. In so doing, we leave terminals unchanged and substitue for each variable of the body any string that is known to be in the language of that variable.
The four components just described form a context-free grammar, or just grammar, or CFG. We shall represent a CFG by its four components, that is, , where is the set of variables, the terminals, the set of productions, and the start symbol.
2.2 Chomsky Normal Form
Theorem
If is a CFG generating a language that contains at least one string other than , then there is another CFG such that , and has no -productions, unit productions, or useless symbols.
We complete our study of grammatical simplifications by showing that every nonemtpy CFL without has a grammar in which all productions are in one of two simple forms, either:
, where , and , are each variables, or
, where is a variable and is a terminal.
Further, has no useless symbols. Such a grammar is said to be in Chomsky Normal Form, or CNF.
Theorem
If is a CFG whose language contains at least one string other than , then there is a grammar in Chomsky Normal Form, such that .
2.3 Parse Trees
Let be a CFG. If the recursive inference procedure tells us that terminal string is in the language of variable , then there is a parse tree with root and yield .
Theorem
Suppose we have a parse tree according to a Chomsky-Normal-Form grammar , and suppose that the yield of the tree is a terminal string . If the length of the longest path is , then .
2.4 The Pumping Lemma for Context-Free Languages
The pumping lemma for CFL's is quite similar to the pumping lemma for regular languages, but we break each string in the CFL into five parts, and we pump the second and fourth, in tandem.
Let be a CFL. Then there exists a constant such that if is any string in such that is at least , then we can write , subject to the following conditions:
. That is, the middle portion is not too long.
. Since and are the pieces to be "pumped", this condition says that at least one of the strings we pump must not be empty.
For all , is in . That is, the two string and may be "pumped" any number of times, including , and the resulting string will still be a member of .
Proof: Our first step is to find a Chomsky-Normal-Form grammar for . Technically, we cannot find such a grammar if is the CFL or . However, if then the statement of the theorem, which talks about a string in surely cannot be violated, since there is no such in . Also, the CNF grammar will actually generate , but that is again not of importance, since we shall surely pick , in which case cannot be anyway.
Now, starting with a CNF grammar such that , let have variables. Choose . Next suppose that in is of length at least . Because any parse tree whose longest path is of length or less must have a yield of length or less. Such a parse tree cannot have yield , because is too long. Thus, any parse tree with yield has a path of length at least .
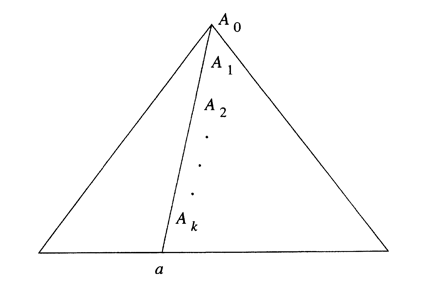
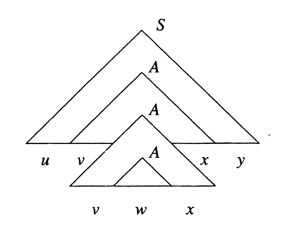
Figure above suggests the longest path in the tree for , where is at least and the path is of length . Since , there are at least occurrences of variables on the path. As there are only different variables in , at least two of the last variables on the path (that is, through , inclusive) must be the same variable. Suppose , where .
Then it is possible to divide the tree as shown in Figure bellow.
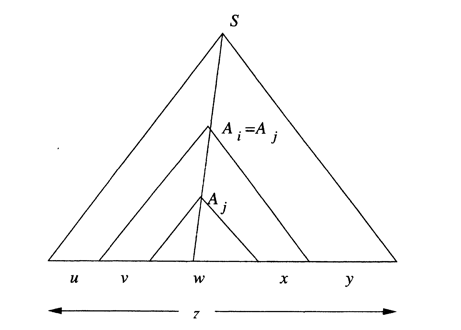
String is the yield of the subtree rooted at . String and are the strings to the left and right, repectively, of in the yield of the larger subtree rooted at . Note that, since there are no unit productions, and could not both be , although one could be. Finally, and are those portions of that are to the left and right, respectively, of the subtree rooted at .
If , then we can construct new parse trees from the original tree, as suggested in Figure bellow (a). First we may replace the subtree rooted at , which has yield , by the subtree rooted at , which has yield . The reason we can do so is that both of these trees have root labeled . The resulting tree is suggested in Figure bellow (b); it has yield and corresponds to the case in the pattern of strings .
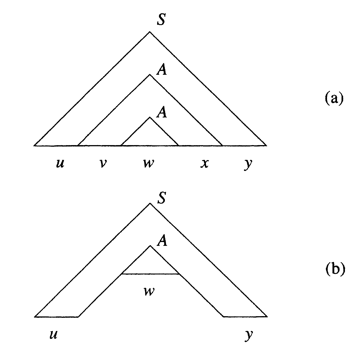
Another option is suggested by Figure bellow. There, we have replaced the subtree rooted at by the entire subtree rooted at . Again, the justification is that we are substituting one tree with root labeled for another tree with the same root label. The yield of this tree is . Were we to then replace the subtree of Figure below with yield by the largar subtree with yield , we would have a tree with yield , and so on, for any exponent . Thus, there are parse trees in for all strings of the form , and we have almost proved the pumping lamma.
The remaining detail is condition (1), which says that . However, we picked to be close to the buttom of the tree; that is . Thus, the longest path in the subtree rooted at is no greater than . Because the subtree rooted at has a yield whose length is no greater than .