递归函数（七）：不动点算子

发表于 | 分类于

回顾

以上几篇文章中，我们讨论了可计算性理论相关的一些内容，

可计算性与递归函数论存在着千丝万缕的联系，

不动点理论也是这样的，我们定义的递归函数一定存在吗？

在什么情况下它是存在的？


要回答以上这些问题，还要从方程，不动点，不动点算子说起。


约束方程



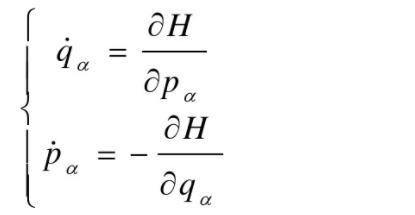
在中学时代，我们学过“方程”的概念，

方程可以简单表述为含有未知数的等式，例如，。

未知数可以同时出现在等式的两边，例如，。

通过合并同类项，我们可以求解。


在大学时代，我们还学过线性方程组和微分方程，

例如，求解矩阵的特征值和特征向量，

二阶常微分方程（贝塞尔方程），。


在计算机科学中，同样的未知“数”的思想，

还出现在了类型推导（例如：unification）与递归函数的定义中。


以上这些例子，方程是“约束”的一种表现形式。


我们回到最简单的阶乘函数fact的定义式，

1
2
3
fact :: Int -> Int
fact 1 = 1
fact n = n * fact (n-1)


去掉语法糖，稍微修改一下，

1
2
3
4
fact :: Int -> Int
fact n = case n of 
  1 -> 1
  n -> n * fact (n-1)


我们发现，fact的定义和“方程”十分相似，fact同时出现在了等式的两边，

阶乘函数，就是这个“方程”的“解”。


函数的不动点



在中学数学中，我们已经学过不动点了，只是当时印象不是那么深刻，

函数的不动点，是指被这个函数映射到其自身的那些点。

例如：，

则是函数的一个不动点，。


并不是每一个函数都有不动点，

例如，实数域上的函数，就没有不动点，对于任意实数，永远都不等于。

（不动点是和定义域有关的，以后我们还会重新讨论的不动点。


一般的，函数的不动点，指的是这样的，使得。


重新温习了不动点相关的知识之后，

我们就可以对上面的阶乘函数进行改造了，

我们要把阶乘函数看做另外一个函数的不动点。


定义函数，

1
2
3
4
g :: (Int -> Int) -> Int -> Int
g f n = case n of 
  1 -> 1
  n -> n * f (n-1)

我们可以得到，g fact = fact，

因此，fact实际上就是函数g的不动点。


于是，在“方程”中求解fact的过程，

就转换成了求解函数g的不动点的过程了。


不动点算子



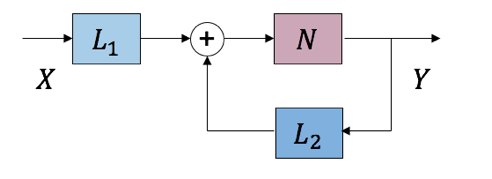
我们怎样求解函数g的不动点呢？

在Haskell中，可以很方便的定义一个高阶函数fix，它可以用来求解任意函数的不动点，

1
2
fix :: (a -> a) -> a
fix g = let x = g x in x


我们试验一下fix的强大威力，

1
2
3
4
5
fact 10
> 3628800

fix g 10
> 3628800


注意，fix g得到的是g的不动点，而不是fact的不动点，

即(fix g) = g (fix g)。


有了fix，我们就可以构造匿名递归函数了，

1
2
3
4
fact' :: Int -> Int
fact' = fix $ \fact -> \n -> case n of 
  1 -> 1
  n -> n * fact (n-1)

fix后面跟的函数没有名字，它是匿名的，但是经过fix作用后，可以产生一个递归函数。

也就是说，为了实现递归，函数是可以没有名字的。


Y组合子



Y组合子，是Haskell B. Curry在研究演算时发现的，

它的表现形式如下，


在演算中，（转换和规约

我们可以证明，对于任何函数g，。


因此，Y组合子是一个不动点算子，它可以得到任意函数的不动点。

其他的不动点算子还有图灵不动点组合子，


讨论Y组合子在Haskell中的表示方式是有趣的，因为直接翻译过去会报类型错误，

1
2
3
4
5
6
7
8
y :: (a -> a) -> a
y = \f -> (\x -> f (x x)) (\x -> f (x x))

-- Occurs check: cannot construct the infinite type: r0 ~ r0 -> a
-- Expected type: r0 -> a
--   Actual type: (r0 -> a) -> a
-- In the first argument of ‘x’, namely ‘x’
-- In the first argument of ‘f’, namely ‘(x x)’

类型系统无法确定x的类型。


问题出在表达式x x上面，

假设x x的类型为a，则第一个x的类型就应该为? -> a，

于是，第二个x的类型肯定也应该是? -> a。（因为都是x


又因为x x的类型为a，

所以第一个x的类型? -> a中，?的类型就应该是? -> a，

（因为((? -> a) -> a)作用到(? -> a)才能得到a


?的类型是? -> a，因此?应该是一个递归类型。


下面我们来定义递归类型Mu，来帮助编译器进行恰当的类型推导，

1
2
3
4
newtype Mu a = Mu (Mu a -> a)

y :: (a -> a) -> a
y f = (\h -> h $ Mu h) (\x -> f . (\(Mu g) -> g) x $ x)


最后，fact'就可以使用Y组合子来定义了。

1
2
3
4
fact' :: Int -> Int
fact' = y $ \fact -> \n -> case n of 
  1 -> 1
  n -> n * fact (n-1)


总结

本文从简单的“方程”思想出发，引出了不动点的概念，

然后把递归函数看做了另外一个函数的不动点，

最后，我们讨论了Y组合子这样一个具体的不动点算子。


可是，这里隐藏着一个问题，我们看到fix是可以求解任意函数的不动点的，

而对于以下递归函数succ，即，

1
2
succ :: Int -> Int
succ n = n+1

在实数域上是显然没有不动点的。


那么fix succ是什么呢？

这个问题，我们将在后文中继续讨论。


参考

方程

特征值和特征向量

微分方程

不动点

不动点组合子

Haskell/Fix and recursion

Y Combinator in Haskell