回顾
上一篇中,我们通过引入极小化算子定义了递归函数,
使用递归函数,我们又定义了递归集与递归可枚举集,
本文我们要讨论,为什么递归可枚举集是“可枚举”的,以及什么是可计算函数。
可计算性
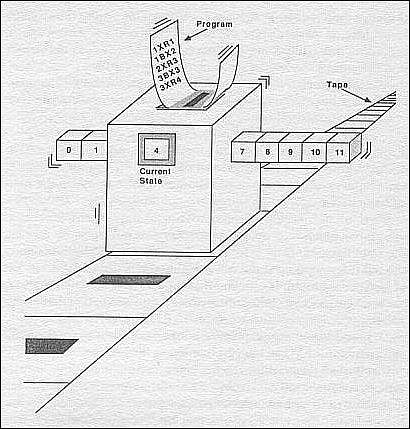
我们听说过,现代计算机在计算能力上是与图灵机等价的,
什么叫做计算能力呢?
它指的是图灵机可计算的函数集,与现代计算机可计算的函数集是相等的。
为了简单起见,我们不去讨论图灵机,而是从现代计算机直接说起,
设是一段程序,是一个正整数,
我们称数论函数为程序所计算的元部分函数,
如果对于相同的输入,
要么:(1)程序的计算可以终止,此时计算结果等于的相应函数值;
要么:(2)程序的计算不能终止,此时无定义。
设是一个部分函数,如果存在程序可计算,则称是部分可计算的。
如果一个函数,既是部分可计算的,又是全函数,则称这个函数是可计算的。
可以证明,所有的原始递归函数和递归函数都是部分可计算的。
通用程序
我们使用现代计算机进行编程的时候,并不是直接把程序的输入传给程序,
而是将程序本身以及它的输入,传给计算机,最后由计算机得到计算结果,
像这种接受任何程序和它的输入作为自己的输入,返回程序执行结果的程序,称为通用程序。
为此,通用程序需要把输入的程序进行编码。
为了不引入太多的复杂性,我们可以将程序的编码理解为存储程序的二进制数据,
不同的程序会有不同的二进制表示,每一个二进制表示可以对应一段程序(虽然可能不合法)。
哥德尔编码做的事情就是将程序和自然数集一一对应起来。
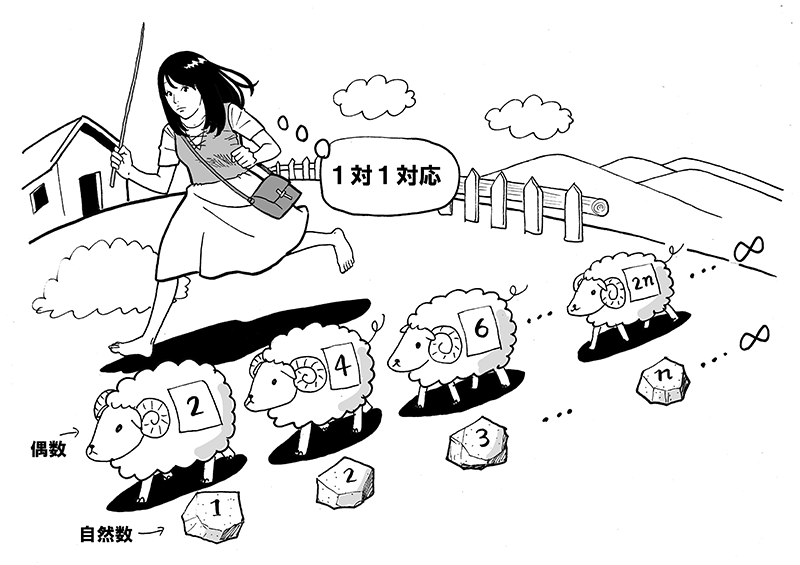
因此,所有程序的个数是可数的,而这些程序可计算的函数个数也一定是可数的,
它们可能是全函数,也可能是部分函数。
(其中,“可数”指的是可数集,可数集是与自然数集之间存在一一映射的集合。
然而,自然数集上的函数全体并不可数,(证略
所以肯定存在程序不可计算的函数。
集合个数的可枚举性

程序所计算的函数,我们可以记为,
由此,我们可以定义通用程序,则有,
其中,是程序的编码。
因为,所有的程序与自然数集一一对应,
所以,
枚举了所有的元可计算函数。
我们定义,
根据递归可枚举集的定义,每一个是一个递归可枚举集。
又因为枚举了所有的可计算函数,
而上一篇中我们看到,递归可枚举集是由部分递归函数(即,可计算函数)定义的,
一个部分递归函数确定出一个递归可枚举集,
所以,枚举了所有的递归可枚举集。
因此,集合是递归可枚举的,当且仅当存在,使得,
称为枚举定理,这就是“枚举”的含义。
令,
则是递归可枚举的,但不是递归的,(证略
因此,不是递归可枚举的,否则就是递归集了。
(根据,集合是递归的当且仅当和是递归可枚举的,见上一篇
因此,我们找到了一个非递归的递归可枚举集,
以及一个非递归可枚举集。
停机问题
任给一个程序和一个自然数,问该程序对这个自然数输入的计算是否停止,
这个问题称为停机问题。
我们可以用谓词描述这个问题,
,表示以为代码的程序对输入的计算最终停止。
那么,是不可计算的,即,不存在一个程序来计算。
我们来证明一下,假设有一个程序可以计算,
那么我们就能用它来构造一个新程序,它的输入是,
这段程序当为真时,计算不停止,而当为假时,计算停止。
程序也可以进行编码,假设为,现在我们来判断。
如果为真,意味着编码为的程序以作为输入最终停止,
即程序,输入为时,最终停止,
可是根据的定义,此时为假才会停止,矛盾。
如果为假,意味着编码为的程序以作为参数最终不会停止,
即程序,输入为时,最终不停止,
可是根据的定义,此时为真才不会停止,矛盾。
不能为真也不能为假,矛盾,
因此,计算的程序不存在,我们也无法用它来构造程序。
可判定性

可判定性问题,指的是一个询问真或者假的问题是否可以被回答。
如果我们总能回答出这个问题是真或者是假,就称该问题是可判定的,
如果我们只能当问题为真的时候确定为真,为假的时候所进行的计算可能不会终止,那么就称该问题是半可判定的。
某元素是否属于一个递归集,是可判定的,
某元素是否属于一个递归可枚举集,是半可判定的。
因为,递归集是使用一个递归的全函数定义的,
而递归可枚举集是使用第一个部分递归函数定义的,
我们无法判断某个部分递归函数,在接受某参数时,是没有定义,还是计算尚未停止。
即,判断元素是否属于某递归可枚举集的程序可能永不停机。
总结
本文介绍了函数的可计算性,通用程序,以及最多有多少个程序,
还了解了停机问题和可判定性问题。
这些都是可计算性理论的基础,我们清晰的看到了人类的计算能力,
以及用递归所能计算的函数范围,后文中我们开始讨论不动点理论,
这同样是一个有趣的话题。
附
配对函数和哥德尔数,是对数偶和有穷数列的一种编码方式。
(1)配对函数
令,称为配对函数,它是一个原始递归函数。
任给一个数,存在唯一的一对数和,使得。
是含有因子的个数,即使得的的最大值。
必为奇数,是的唯一解。
一般的,记,,则和也是原始递归函数。
(2)哥德尔数
记,
称为有穷数列的哥德尔数。
其中,是第个素数。
例如,。
对于每一个固定的,是原始递归函数,并且这种编码具有唯一性。