回顾
上文我们讨论了集合上的关系,还讨论了数学归纳法的一种普遍形式,称为良基归纳法,
它建立在集合上的良基关系之上。
本文开始讨论函数,我们将回顾函数的定义,
然后解释什么是全函数(total function),什么是部分函数(partial function)。
我们会看到,在证明一个递归函数是全函数时,
良基归纳法起到了重要作用。
在分析学中,人们似乎很少关心函数的完全性,
只关心它的连续性,可导性,可微性与可积性,等等。
而在计算机科学领域中,人们更在意计算的可终止性,
因此一个函数在某个点是否有定义将经常被提及。
程序中定义的函数,往往对应于某个集合上的数学函数,
为了描述程序的非终止性,就得扩充这个数学函数的定义域和值域。
为了理解这些事情,我们先要从函数的定义开始。
函数
集合上的关系,是笛卡尔积的一个子集。
而函数,则是集合上的一种特殊关系,
它要求中的每一个元素,都有中唯一确定的元素与之对应。
其中,集合称为函数的定义域,集合称为函数的值域。
函数是我们熟悉的概念,这里只是提到了它本质上是集合上的一个关系。
(1)部分函数(partial function)
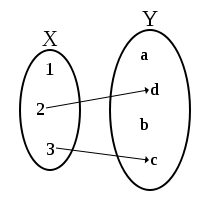
如果是从到的二元关系,且,或,
则称是从到的部分函数,或上的部分函数。
其中,如果,则称有定义,记为,
也称为在点的函数值,记为。
如果,则称无定义,记为。
(2)全函数(total function)
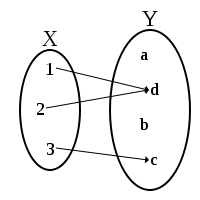
如果都有,则称是上的全函数,
此时,可以记为。
可见,我们熟悉的函数,指的是全函数。
值得注意的是,部分函数的定义已经包含了我们学过的“函数”的定义,
后文中,我们提到的“函数”如果不强调它的完全性的话,都泛指部分函数。
非终止性
部分函数在计算机科学中是非常重要的,
因为对于每一个,一个算法可以表示为,计算出集合中与之对应元素的过程,
这个算法可能对于某些值不会终止,而这种情况是很常见的。
例如:
1 | f :: Int -> Int |
这样定义的函数f,对应了数学上的一个部分函数,它只在某些情况下有意义,
只有当n是奇数时,我们才能得到终止性的结果。
而当n是偶数时,算法会无限的递归下去,直到堆栈溢出。
因此,将Int解释为整数集,将f :: Int -> Int解释为整数集上的函数,似乎是有问题的。
因为,并不是一个整数,它的计算不能终止。
为了描述非终止性,就需要对整数集进行扩充,
我们给整数集加上一个特殊元素“”,称为bottom,来表示非终止性,
而将f :: Int -> Int解释为集合上的一个数学函数。
像这种通过构造表达程序含义的数学对象,来对程序进行分析的方法,来自指称语义学。
指称语义中,人们会区分函数的严格性,一个函数称为严格的(strict),
如果接受一个非终止的输入表达式,函数的计算仍然不会终止,
即,。
否则,称函数为不严格的(non-strict)。
原始递归函数
我们看到在程序中使用递归,可能会导致非终止性的计算,而有些递归又不会。
这是为什么呢?
我们可以从递归函数论中找到一些线索。
递归函数论是和图灵机以及演算相等价的计算模型,它从另一个角度刻画了可计算性。
可计算性是一个有趣的话题,后续文章中,我们会详细讨论。
在递归函数论中,人们把函数划分为了3个层次,
原始递归函数,递归函数,和其他的不能用递归函数表示的“函数”。
这些函数集合的范围越来越大。
本文我们先介绍原始递归函数,
为此,我们需要先定义两种运算。
(1)合成运算
设是元部分函数,是个元部分函数,令,
则称是由和,经过合成运算得到的。
(2)原始递归运算
设是一个元全函数,是元全函数,令,
则称是由和经过原始递归运算得到的。
于是,我们就可以定义原始递归函数了。
设初始函数包括,
(1)零函数
(2)后继函数
(3)投影函数,
则由初始函数经过有限次合成运算和原始递归运算得到的函数,称为原始递归函数。
原始递归函数有以下这些性质:
由原始递归函数经过合成或原始递归得到的函数仍为原始递归函数,
因此,原始递归函数的集合在合成与原始递归运算下是封闭的。
此外,每一个原始递归函数都是全函数。
这是因为合成运算虽然是在部分函数上定义的,
但是如果和是全函数,那么也一定是全函数。
另一方面,在进行原始递归运算时,如果和是全函数,则也一定是全函数,
这是因为原始递归运算在的参数集上的定义了一个良基关系,由良基归纳法可证,是全函数。
总结
本文介绍了全函数与部分函数,以及计算可终止性相关的概念,
我们对程序中函数的指称,进行了定义域和值域的扩充,
随后,我们进一步了解了原始递归函数,以及它的完全性,良基归纳法起到了关键作用。
下文,我们将深入到可计算性理论,
讨论部分可计算函数和可计算函数的区别,讨论递归函数与原始递归函数的关系,
引出递归可枚举集这个重要的概念。