回顾
上文我们讨论了集合上的偏序结构,之所以谈论它们是因为,
完全偏序集上的连续函数具有最小不动点,这称之为最小不动点定理,
除了集合论的一些知识之外,我们还要讨论到底什么是连续函数,以及什么是完全偏序集。
有向子集与完全偏序
偏序集的非空子集叫做有向子集(directed subset),
当且仅当,对于中的任意元素,
存在中的一个元素,有且。
如果一个偏序集的每个有向子集都有上确界(记为),
就称它是一个有向完全偏序集,
此外,如果它还有最小元,就称它是一个完全偏序集。
注意,完全偏序集并不是每一个子集都有上确界,
而是它的每一个有向子集都有上确界。
连续函数

假设与是完全偏序集,
是集合上定义的一个函数,
如果,则为的子集,
其中。
对于任意的,如果就有,
我们就说是单调的。
可以看出,如果是单调的,且是的有向子集,那么也是的有向子集。
如果是单调的,且对于任意有向子集,
有,就称是连续的。
连续函数集上的偏序结构
完全偏序集到的连续函数,也可以定义出一个偏序结构,
我们称,当且仅当对于每一个,我们有。
这样我们就得到了一个元素为连续函数的偏序集,。
可以证明,也是一个完全偏序集。(证略
最小不动点定理
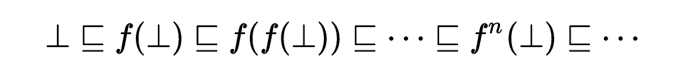
如果是一个完全偏序集,且是连续的,
则有最小不动点,。
因为是中的最小元,且,所以,,
因为是连续的,所以也一定是单调的,所以,,
继而,,对于任意的都成立。
构成了一个全序集,
所以,它是完全偏序集的一个有向子集,必有上确界。
设是上确界,,
则是的不动点,因为,由的连续性,
,
而与有同样的上确界,
所以,,即是的不动点。
其次,是的最小不动点,
假设是的任意不动点,因为,所以,
类似的,对于任意的,。
而是的不动点,所以,
因此是集合的上界。
由于集合的最小上界是,所以有。
后继函数的不动点

1 | succ :: Int -> Int |
在第七篇中,我们说fix可以得到任意函数的不动点,
那么这个succ函数呢?它有没有不动点?
fix succ是什么?
现在我们有了最小不动点定理,
就得验证succ所指称的数学函数,是不是一个完全偏序集上的连续函数,
如果是的话,它就有不动点。
在第四篇为了表示计算的不可终止性,我们对自然数集进行了扩充,,
然后用这个集合作为程序中Int类型的值的解释。
然而,不是一个完全偏序集,原因是它没有上界,
如果我们额外加入一个比其他的自然都大的元素,
则我们就得到了一个完全偏序集,。
然后,我们看succ连续吗?
首先,它是单调的,如果我们再定义,
就有,
因此,succ是一个连续函数。
根据最小不动点定理,succ的最小不动点是,。
由于,即对于非终止的输入succ的计算也不会终止,
所以,
因此,,
即,succ的最小不动点是,fix succ的计算不会终止。
求解阶乘函数
上一篇中,我们证明了阶乘函数fact是以下函数的不动点,fact = fix g,
1 | g :: (Int -> Int) -> Int -> Int |
现在我们来看一下,如何运用最小不动点定理来得到这个答案。
为了避免篇幅过长,关于g函数的连续性证明暂略,
我们直接使用公式,
,
即,g函数的最小不动点,就是集合的上确界。
我们先来看一下这个集合中有哪些元素,
其中,,我们将传入中,看看会得到什么,
1 | f1 = \n -> case n of |
这个函数能计算f1 1,但是不能计算f1 2,恰好是fact函数有限展开的一阶项。
我们再来看,它等于,
1 | f2 = \n -> case n of |
这个函数能计算f2 1以及f2 2,但是不能计算f2 3,恰好是fact函数展开的二阶项。
由此,我们看出了规律,
就是fact函数有限展开的第阶项。
上一篇中,我们已经证明了,当时,它就是fact函数,
考虑到这些函数的序关系,
因此,我们有。
即,fact函数就是g函数的最小不动点。
总结
到此为止,我想这个系列的文章已经讨论完了,
本系列文章一直围绕着递归函数和不动点进行分析,
在内容上可以分为两个部分,前半部分主要与可计算性理论有关,
后半部分与不动点定理有关,希望对大家有所帮助。