回顾
上一篇我们介绍了不动点算子和Y组合子,以及Y组合子的具体表现形式,
这一篇我们根据不动点算子的性质来证明fact函数就是g函数的不动点。
随后,我们回归到了数学中,讨论集合上的一种偏序结构,
这为下文完全偏序集,以及完全偏序集上连续函数的不动点定理做好准备。
不动点算子的性质
上文我们介绍了不动点算子fix,
它可以用来求取任意函数的不动点。
1 | fix :: (a -> a) -> a |
并且我们说以下函数的不动点为fact = fix g,
1 | g :: (Int -> Int) -> Int -> Int |
但是上文中,我们只是对它们的计算结果进行比对,
并没有对它进行证明。
考虑到fix的性质,fix g = g (fix g),
(因为fix g是g的不动点,令h = fix g,上式为h = g h
我们可以使用数学归纳法,证明对于任意的自然数,fact n = fix g n。
我们先证初始条件,
1 | fix g 1 |
然后再证递推条件,假设fact k = fix g k,
我们要推出fact (k+1) = fix g (k+1),其中,。
1 | fix g (k+1) |
因此,对于任意的自然数,fact n = fix g n。
即,fact = fix g。
不动点算子的有限展开
根据上一节fact = fix g的证明,我们看到,
每一步递推,我们都使用了不动点算子fix的性质fix g = g (fix g),
但是对于一个具有有限存储空间的机器来说,递推的步骤不可能是无限的,
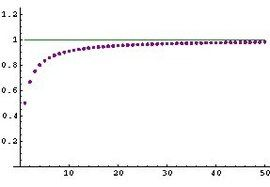
为了界定最多使用多少次递推,我们定义,。
并且认为对于任意的无定义。
,而在时没有定义,
,,而在时没有定义。
因此,是一个部分函数,且,
所表示的函数,总是比的计算能力更强一些,离fact更近一些。
当时,就是阶乘函数fact。
即,的最小上界,就是g的不动点。
那么,什么样的g才能保证这个集合具有最小上界呢?
序理论指出,完全偏序集上的序保持自映射具有最小不动点。
为此,我们需要先认识什么是偏序集,什么是连续函数。
使用完全偏序集上的连续函数解释程序中函数的方式,称为域论模型。
偏序集与哈斯图
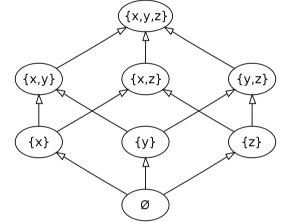
在第三篇中,我们讨论过偏序关系,
一个偏序集是一个集合,
并且在这个集合上定义了一个偏序关系。
设为实数集的一个非空子集,我们定义上的偏序关系为,
当且仅当是小或等于的实数。
则,是一个偏序集。
偏序集反映了集合上的一种偏序结构,它比我们想象中的更为常见,
例如,一个集合,对于任意两个元素,我们定义当且仅当。
那么是一个偏序集。
因此,如果某个集合构成了一个偏序集,这完全取决于我们怎样定义偏序关系。
设是一个偏序集,
对于任意的,如果总是有或者成立,
则称和是可比的。
,且,则记为。
如果和是可比的,且,如果不存在,使得,则称覆盖。
根据可比性和覆盖性,我们就可以将偏序关系用无向图表示出来了,
其中,顶点表示元素,边表示覆盖关系,并且省去图中每个顶点处的环,
覆盖就将代表的顶点放在代表的顶点之上,并在和之间连线,
如果,但是不覆盖,就省掉与之间的连线。
这样用来表示有限偏序集的无向图,称为哈斯图。
例如,易证整除关系是整数集上的一种偏序关系,
我们可以画出偏序集对应的哈斯图,如下,
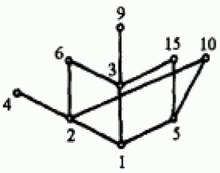
全序集与拟序集

设是一个偏序集,如果对于任意,和都可比,
则称为上的全序关系,此时称为全序集。
可见,实数集以及实数集上的小于等于关系,构成了一个全序集。
哈斯图为从下至上的“一条线”,是全序集的充要条件。
设是非空集合上的,反自反的和传递的二元关系,
则称为上的拟序关系,常将拟序关系记为,并称为拟序集。
拟序关系自然具有反对称性。
(其中,反自反关系,指的是不存在,使得。
拟序关系与偏序关系的哈斯图在画法上完全相同,只是拟序关系的哈斯图的各顶点都没有环。
设是一个拟序集,如果对于任意的,
,,三式有且仅有一式成立,则称具有三歧性,
这样的拟序关系,称为拟全序关系,这样的拟序集,称为拟全序集。
拟全序集的哈斯图也是“一条线”。
最小元与上确界
对于偏序集,以及它的一个子集,
如果存在,且对于任意的,有,
则称为的最小元。(相似的我们可以定义最大元
如果存在,对于任意的,
如果那么就有,
则称为的极小元。(相似的我们可以定义极大元
如果是有穷集,则的极小元一定存在,并且可能有多个,
但是最小元却不一定存在。
上文中,我们画出了偏序集对应的哈斯图,
我们取,,,
则是的最小元,也是极小元,是的极大元,但没有最大元。
是的极小元,但没有最小元,是的最大元,也是极大元。
是的最小元,也是极小元,是的极大元,但是没有最大元。
对于偏序集,以及它的一个子集,
如果存在,(注意,不一定是
使得对于任意的,,则称为的上界,
如果的所有上界存在最小元,则称它为最小上界,或上确界。
(相似的可以定义下确界
的上界和下界不一定存在,即使存在,上确界和下确界也不一定存在。
设是一个拟全序集,如果对于中的任何非空子集都有最小元,
则称是一个良序关系,是一个良序集。
例如,自然数集以及自然数集上的小于关系,构成了一个良序集,
但是,整数集以及整数集上的小于关系,并不构成良序集,而仅仅是一个拟全序集。
总结
本文从一个证明出发,我们了解了不动点算子的工作原理,
然后引出了一些数学概念,序关系在不动点算子理论中占有很重要的地位,
所以,这里给出了详细的介绍,下文我们开始讨论最小不动点定理。