
回顾
上文我们介绍了Henkin模型,以及它的环境模型条件和组合模型条件,
它们分别为合法的项和项,找到了对应的语义解释。
然而这只是简单类型化演算的其中一种解释。
另一种常用的解释方式,建立在范畴论基础之上,称为笛卡尔闭范畴。
为了理解这个概念,我们需要补充一些简单的范畴论方面的内容。
1. 数学结构

范畴论的研究数学结构的形式化方法,
它不考虑具体的数学对象,而是考虑数学对象以及它们之间的联系。
学习范畴论最好的办法,我认为不宜马上从抽象的概念开始,
而是先回到具体的例子上面,找到相似性,理解概念被发明的动机。
因此,我们要先理解什么是数学结构。
后文中,我们会首先介绍最常被提及的群结构,然后再介绍拓扑空间和CPO(完全偏序)。
有了这些例子之后,对抽象概念的理解是事半功倍的。
2. 群结构
群是一种满足结合律的乘法结构,
但是它的运算对象,却并不局限于整数,有理数甚至实数上。
因此,群论对概念采用了不同的定义方式,和初等代数有明显的不同。
在初等代数中,我们研究的是具体的运算系统,
例如,我们会先介绍什么是自然数,然后再介绍自然数上的四则运算。
群论则不然。
它会先抽象的定义满足哪些条件的运算系统是群,
然后再去寻找(或证明)具体的运算系统满足这些条件。
为此,我们先从条件最弱的半群开始,
逐渐增加约束条件,最终认识群结构是怎么建立起来的。
半群
集合和上满足结合律的二元运算,
所形成的代数结构,叫做半群,记为,
半群运算,也常简记为。
好在我们第二篇中,对“什么是代数”进行了严谨的定义,
因此,对这里提到的“代数结构”应该并不陌生,很显然半群是一个代数。
满足半群条件的例子是非常多的,
例如,自然数集以及自然数上的乘法运算,构成了一个半群。
值得注意的是,集合和运算要放在一起考虑才行,
集合包含了运算对象,运算表明了运算对象之间的关系。
幺半群

设是半群,元素,称为半群的幺元,
如果,。
可以证明,如果半群存在幺元,则必定是唯一的。
幺元常被记为,或者直接写成。
具有幺元的半群,称为幺半群,记为。
幺半群的例子,我们可以考虑字符串及其连接运算,
在连接运算下,空串是幺元。
群
设是幺半群,如果它的每个元素都可逆,我们就称它为群。
所谓可逆指的是,,,
使得,
其中为的幺元。
自然数集以及自然数上的乘法运算组成的代数结构,是半群,
如果把自然数看做幺元,则构成了一个幺半群,但是它不是群。
因为,除了之外,任何自然数都没有逆元。
字符串及其连接运算,构成了一个幺半群,但也不是群,
因为,没有任何两个非空字符串连接在一起会得到空串。
下面我们来看一个群的例子。
如果我们把整数集(包含正负整数)看做运算对象的集合,
把整数集上的加法运算看做群定义中的二元运算,
整数看做加法运算的幺元,则这样的运算系统构成了一个群。
因为,每一个整数的相反数,都是它的逆元。
群同态
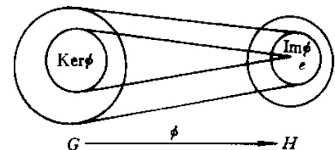
有了群之后,很自然的一步我们会考虑两个群是否足够相似,
这就需要我们找到两个群之间的对应关系。
设和是两个群,
我们把映射称为群同态,如果,
都有。
如果是单射,则称为单同态,
如果是满射,则称为满同态。
如果是双射,则称为群同构。
同构的两个群,记为。
小结
现在我们理解了半群,幺半群,群,群同态,
这些概念放在一起,就是所谓的群结构。
结构一般所指的是一些运算规则,或者约束条件。
为了更好的理解数学结构,
下面我们来介绍另一个概念,它来自拓扑学,称为拓扑空间。
3. 拓扑结构

拓扑学,被人们戏称橡皮膜上的几何学,
它主要研究在连续变换下保持不变的几何性质,
例如,连通性和紧致性。
这里我们先不展开,
主要看一下在拓扑学中是怎么建立数学结构的。
子集族
设是一个非空集合,是的幂集(所有子集构成的集合),
把的子集(即以的一部分子集为成员的集合)称为的子集族。
拓扑空间
设是一个非空集合,的一个子集族称为的一个拓扑,
如果它满足
(1)和都包含在中
(2)中任意多个成员的并集仍在中
(3)中有限多个成员的交集仍在中
集合和它的一个拓扑一起称为一个拓扑空间,记作。
称中的成员为这个拓扑空间的开集。
从定义看出,给出集合的一个拓扑就是规定它的哪些子集是开集。
连续映射

设和都是拓扑空间,是一个映射,
,如果对于包含的每一个开集,必存在包含的开集,
使得,,则我们就说,在处连续。
如果映射在任一点都连续,
则说是连续映射。
同胚映射
如果是双射,
并且及其逆都是连续的,
则称是一个同胚映射,简称同胚。
当存在到的同胚映射时,就称与同胚,
记作。
值得注意的是,同胚映射中条件连续不可忽视,
它不能从双射和的连续性推出来。
小结
以上我们介绍了拓扑空间,以及两个拓扑空间之间的连续映射,
这和群以及两个群之间的群同态是很相似的。
它们表现出了一种结构上的相似性,
范畴论正是看到这种相似性,于是跳出具体的运算系统,
例如,它可以考虑群结构与拓扑结构之间的关系。
接下来我们来介绍CPO(完全偏序)。
它在范畴论中,对于摆脱集合论的观念束缚,帮助是很大的。
4. 完全偏序
在《递归函数》系列文章中,
我们已经介绍过CPO(完全偏序)的概念了。
为了方便与本文中其他概念进行对比,我们再简单的梳理一下。
二元关系
集合和上的二元关系,
指的是它们笛卡尔积的子集,。
自反性,对称性,反对称性,传递性
一个二元关系是自反的,如果对于所有的成立;
是对称的,如果就有,对于所有的都成立;
是反对称的,如果且,则是同一个元素,对于所有的都成立;
是传递的,如果和能推出,对于所有的都成立。
偏序关系
等价关系是同时具有自反性,对称性和传递性的关系。
偏序关系是具有自反性,反对称性和传递性的关系。
等价关系的一个例子就是相等性,
相等性关系当且仅当是同一个元素。
偏序关系,例如通常的序关系,
当且仅当。
最小元与上确界
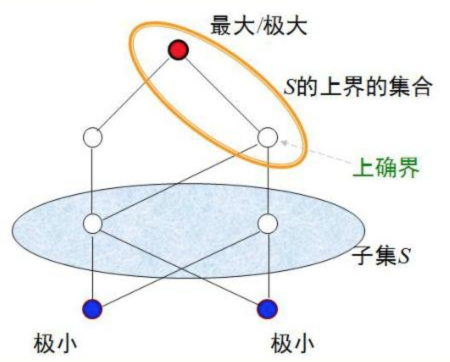
对于偏序集,以及它的一个子集,
如果存在,且对于任意的,有,
则称为的最小元。
对于偏序集,以及它的一个子集,
如果存在,(注意,不一定在子集中)
使得对于任意的,,则称为的上界,
如果的所有上界存在最小元,则称它为最小上界,或上确界。
完全偏序集
偏序集的非空子集叫做有向子集,
当且仅当,对于中的任意元素,
存在中的一个元素,有且。
如果一个偏序集的每个有向子集都有上确界(记为)
就称它是一个有向完全偏序集,
此外,如果它还有最小元,就称它是一个完全偏序集。
注意,完全偏序集并不是每一个子集都有上确界,
而是它的每一个有向子集都有上确界。
连续函数
假设与是完全偏序集,是集合上定义的一个函数,
对于任意的,如果就有,
我们就说是单调的。
如果是单调的,且对于任意有向子集,
有,就称是连续的。
小结
我们又重新回顾了完全偏序这一概念,
实际上,任意一个CPO(完全偏序),都构成了一个范畴,
而所有的群,也构成了一个范畴。
群范畴的对象是集合,而CPO(完全偏序)范畴的对象不一定是集合。
这对摆脱集合论来理解范畴是很关键的。
总结
本文介绍了三种数学结构,群结构,拓扑结构,以及CPO(完全偏序)。
作为例子,可以为后面学习范畴论打下扎实的基础。
我们看到了这些数学结构之间的相似性,
从下一篇开始,我们要开始范畴论的学习之旅了。