自然数归纳法

自然数归纳法,是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。
它可以用一个有限的方式写出一个无限的证明。
后续文章中我们会看到,这种用有限表示无限的方法,其实是有局限性的,并不能用来解决所有的问题,
它能处理的只是无限中的一个子集罢了。
自然数归纳法,我们可以描述如下:
为证明对每一个自然数,命题为真,只需要证明两件事,
(1)对于自然数,命题为真
(2)如果对于自然数,命题为真,那么对于自然数,命题也为真
其中,第(1)条称为起始条件,第(2)条称为递推条件,或者称为归纳步骤。
第(2)条中,为了证明而假设的,称为归纳假设。
这似乎是很显然的事情,我们可以在一张无限长的纸带开头写上初始条件,
接着根据递推条件,由我们可以证明成立,
重复这种思想,我们可以由证明成立,如此不断的进行下去,
最终,对于每个自然数,我们都能证明成立。
但是,这样并不算是一个有效的证明。
要证明自然数归纳法的正确性,我们还需要补充一些集合论方面的知识。
然而,在此之前,我们还是先来看自然数归纳法的一个例子吧。
例子

在上一篇,我们在定义递归函数fact的时候,
先找到了“递推式”,再找到了“终止条件”,然后写出了fact的定义:
1 | fact :: Int -> Int |
我们还提到,有一个步骤是必不可少的,
那就是证明fact的正确性,即证明这样定义的fact就是阶乘函数。
现在,我们正好可以用自然数归纳法来证明它。
我们假设命题为:fact n的值为
(1)对于自然数,命题:fact 1的值为,成立
(2)假设对于自然数,命题:fact m的值为,成立;
那么,我们可以得到fact (m+1) = (m+1) * fact m,值为,也成立。
所以,对于任意自然数(),fact n的值就是。
于是,我们证明了fact就是阶乘函数。
自然数归纳法还有另外一种等价形式,
如果要证明对每一个自然数为真,
只要证明对于任意自然数,如果当为真,那么也为真。
集合上的关系
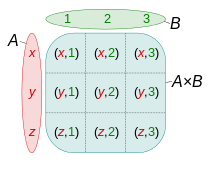
关系是一个日常生活用语,例如,“同学关系”,“我们的关系很好”之类的。
然而,它也是一个集合论中的概念,这给我们带来了很多困扰。
为了避免歧义,本文中从这里开始,我们开始谈论数学,我们要对集合上的“关系”进行定义。
直观的说,集合的元素和集合的元素之间的关系是一个二元性质,
使得对于每个和而言,要么为真,要么为假。
关系通常表示为一个集合,它是笛卡尔积的子集,即,
集合和集合之间的关系是它们笛卡尔积的一个子集。
如果序对属于子集,则认为与之间的关系为真,否则认为与之间的关系为假。
通常关系直接描述为,或者,而不用。
除了二元关系之外,对任何正整数,还可以定义元关系。
如果为集合,则在上的元关系是笛卡尔积的一个子集。
某个集合上的二元关系有很多性质,例如自反性,对称性,反对称性,传递性。
一个关系是自反的,如果对于所有的成立;
是对称的,如果就有,对于所有的都成立;
是反对称的,如果且,则是同一个元素,对于所有的都成立;
是传递的,如果和能推出,对于所有的都成立。
(注意,反对称性不是对称性的否定。
等价关系是同时具有自反性,对称性和传递性的关系。
偏序关系是具有自反性,反对称性和传递性的关系。
等价关系的一个例子就是相等性,相等性关系当且仅当是同一个元素。
偏序关系,例如通常的序关系,当且仅当。
良基关系

归纳法有各种各样的形式,自然数归纳法只是其中的一种应用,
在数理逻辑和形式语言理论中,用的最多的是结构归纳法,在树形结构上进行归纳,后续文章中我们会提到。
人们总结了各种归纳法的共性,提出了良基关系的概念,
于是,自然数归纳法和结构归纳法都变成了在良基关系上通用归纳法的具体应用了。
集合上的良基关系(well-founded relation),是上的一个二元关系,
如果不存在无限下降序列(infinite descending sequence)。
例如,自然数上的关系,就是一个良基关系。
但是却不是,因为存在一个无限下降序列。
根据良基关系,我们可以定义集合中的最小元,
为最小元,如果不存在,使得。
对于良基关系,有一个等价的定义,
上的二元关系是良基的,当且仅当的每一个非空子集有最小元。
我们可以证明一下这两种说法等价性。
要证当且仅当,我们需要证明充分性和必要性,
(1)充分性:
要证:上的二元关系是良基的,则的每一个非空子集有最小元。
使用反证法,如果没有最小元,则对于每个,总可以找到,使得。
但是,如果这样的话,我们就可以对任何,以开始构造一个无限下降序列,
这与是一个良基关系矛盾。充分性证毕。
(2) 必要性:
要证:如果的每一个非空子集都有最小元,则上用于比较的二元关系是良基的。
由于的每一个非空子集都有最小元,则不可能存在无限下降序列,
因此,是良基的。必要性证毕。
因此,上的二元关系是良基的,当且仅当的每一个非空子集有最小元。
良基归纳法

设为集合上的良基二元关系,并且设为关于中元素的某个命题,
如果对于所有的成立,就必然有成立,
那么就对所有的成立。
我们看到确实是自然数集上的良基关系,因此自然数归纳法只是良基归纳法的一种特例。
现在我们有了足够的能力来证明自然数归纳法的正确性了,
只要我们证明了良基归纳法是正确的。
还是用反证法:
我们期望证明,
前提:如果对于所有的成立,必然有成立,
结论:那么对于所有的,都成立。
如若不然,假设存在,使得不成立,
则集合非空,
因此根据良基关系的等价定义,集合必有最小元,
而且,成立。
则根据前提的逆否命题,一定存在,使得成立,
所以,我们有,且,与是的最小元矛盾。
证毕。
由此,我们证明了良基归纳法的正确性。
理解良基关系和偏序关系,是理解递归和不动点算子的第一步。
总结

本文从自然数归纳法出发,补充了一些集合论方面的知识,
让我们熟悉了集合上的几种常用关系,例如,等价关系,偏序关系和良基关系,
这些关系在以后的文章中还会被再次提到。
最后,我们证明了良基归纳法,从而证明了自然数归纳法的正确性。
不知道是否很明显了,递归的步骤和归纳的步骤,简直是太像了,
这一定不是偶然。
在The Little Prover一书中,为了证明递归函数是否全函数(total function),
作者使用了测度(measure)的概念,这实际上定义了参数集上的一个良基关系。
全函数是可计算理论中一个很重要的概念,
到底什么是全函数,什么是测度?下文我们再详细讨论。